Question

13．如图所示，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
（Ⅰ）若PA=PD，求证：平面PQB⊥平面PAD；
（Ⅱ）点M在线段PC上，二面角M-BQ-C为60°，若平面PAD⊥平面ABCD，且PA=PD=AD=2，求三棱锥M-BCQ的体积．

Answer 1

分析 （Ⅰ））由PA=PD，得到PQ⊥AD，又底面ABCD为菱形，∠BAD=60°，得BQ⊥AD，利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD；
（Ⅱ）以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，建立空间直角坐标系，利用向量法能求出存在点M为线段PC靠近P的三等分点满足题意，再利用锥体体积公式求出．

解答 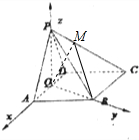（I）证明：∵PA=PD，Q为AD的中点，∴PQ⊥AD，
又∵底面ABCD为菱形，∠BAD=60°，∴BQ⊥AD，
又PQ∩BQ=Q，∴AD⊥平面PQB，
又∵AD?平面PAD，∴平面PQB⊥平面PAD；----------------（6分）
（II）解：∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PQ⊥AD，
∴PQ⊥平面ABCD，
以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，建立空间直角坐标系，如图，则Q（0，0，0），P（0，0，$\sqrt{3}$），B（0，$\sqrt{3}$，0），C（-2，$\sqrt{3}$，0）
设$\overrightarrow{PM}$=λ$\overrightarrow{PC}$，0＜λ＜1，则M（-2λ，$\sqrt{3}λ$，$\sqrt{3}$（1-λ）），
平面CBQ的一个法向量$\overrightarrow{{n}_{1}}$=（0，0，1），
设平面MBQ的法向量为$\overrightarrow{{n}_{2}}$=（x，y，z），
由$\left\{\begin{array}{l}{\overrightarrow{QM}•\overrightarrow{{n}_{2}}=0}\\{\overrightarrow{QB}•\overrightarrow{{n}_{2}}=0}\end{array}\right.$，得$\overrightarrow{{n}_{2}}$=（$\frac{3-3λ}{2λ}$，0，$\sqrt{3}$），
∵二面角M-BQ-C的大小为60°，
∴cos60°=|cos＜$\overrightarrow{{n}_{1}}$，$\overrightarrow{{n}_{2}}$＞|=|$\frac{\sqrt{3}}{\sqrt{（\frac{3-3λ}{2λ}）^{2}+3}}$|=$\frac{1}{2}$，
解得λ=$\frac{1}{3}$，∴MC=2PM，
∴三棱锥M-BCQ的体积=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\frac{2}{3}×\sqrt{3}$=$\frac{2}{3}$．

点评 本题给出特殊四棱锥，求证面面垂直并求锥体体积，着重考查了平面与平面垂直的判定、平面与平面垂直的性质和体积公式等知识，属于中档题．