
分析 (1)利用公式an=Sn-Sn-1判断{an}为等比数列,从而得出通项公式;
(2)求出bn=$\frac{2}{n(n+1)}$,使用裂项求和得出b1+b2+…+bn,从而得出k≤$\frac{n+1}{n}•{2}^{n-1}$,判断新数列{$\frac{n+1}{n}•{2}^{n-1}$}的单调性得出$\frac{n+1}{n}•{2}^{n-1}$的最小值即为k的最大值.
解答 解:(1)n=1时,a1=a2-2,∴a2=a1+2=4.
当n≥2时,an=Sn-Sn-1=an+1-2-(an-2),∴2an=an+1.
即$\frac{{a}_{n+1}}{{a}_{n}}=2$,又$\frac{{a}_{2}}{{a}_{1}}=2$,
∴{an}是以2为首项,以2为公比的等比数列.
∴an=2n.
(2)∵a1a2…an=21+2+3+…+n=2${\;}^{\frac{(n+1)n}{2}}$,
∴bn=$\frac{2}{n(n+1)}$=2($\frac{1}{n}-\frac{1}{n+1}$).
∴b1+b2+…+bn=2(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n}-\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
∵k•(b1+b2+…+bn)≤an,
∴k≤$\frac{n+1}{2n}$•an=$\frac{n+1}{n}•{2}^{n-1}$.
设cn=$\frac{n+1}{n}•{2}^{n-1}$,则cn+1-cn=$\frac{n+2}{n+1}•{2}^{n}$-$\frac{n+1}{n}•{2}^{n-1}$
=2n-1($\frac{2n+4}{n+1}$-$\frac{n+1}{n}$)=2n-1•$\frac{{n}^{2}+2n-1}{n(n+1)}$>0.
∴{cn}为递增数列,∴当n=1时,cn取得最小值2.
∴k≤2.
∴实数k的最大值为2.
点评 本题考查了等比数列的性质,数列求和及数列单调性的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{kπ}{2}$+$\frac{π}{6}$,$\frac{kπ}{2}$+$\frac{5π}{12}$],k∈Z | B. | [$\frac{kπ}{2}$-$\frac{π}{12}$,$\frac{kπ}{2}$+$\frac{π}{6}$],k∈Z | ||
| C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z | D. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
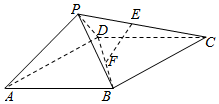 如图,四棱锥P-ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com