
分析 (1)f′(x)=ex(-x2-2x+b).由点P(0,f(0))处的切线方程为y=3x+3.可得f(0)=3,f′(0)=3.解得b,可得函数f(x)的表达式;
(2)由f′(x)<0,f′(x)>0解出可得函数f(x)的单调递减、增区间,即可求出极值点.
解答 解:(1)f′(x)=ex(-x2-2x+b).
∵点P(0,f(0))处的切线方程为y=3x+3.
∴f(0)=3,f′(0)=3.
∴b=3,
∴f(x)=ex(-x2+3).
(2)f′(x)=ex(-x2-2x+3)=-ex(x+3)(x-1),
由f′(x)<0,化为(x+3)(x-1)>0,解得x>1或x<-3,
∴函数f(x)的单调递减区间为(-∞,-3),(1,+∞);单调递增区间是(-3,1)
∴极值点为-3,1.
点评 本题考查了利用导数研究其单调性、极值,考查了推理能力与计算能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:解答题
设椭圆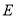 的方程为
的方程为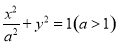 ,
,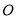 为坐标原点,直线
为坐标原点,直线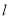 与椭圆
与椭圆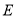 交于点
交于点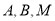 为线段
为线段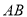 的中点.
的中点.
(1)若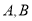 分别为
分别为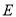 的左顶点和上顶点,且
的左顶点和上顶点,且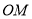 的斜率为
的斜率为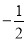 ,求
,求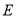 的标准方程;
的标准方程;
(2)若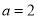 ,且
,且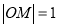 ,求
,求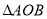 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2017届湖南石门县一中高三9月月考数学(文)试卷(解析版) 题型:解答题
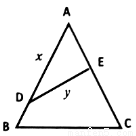
如图,公园有一块边长为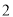 的等边
的等边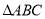 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中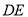 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在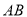 上,
上,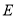 在
在 上.
上.
(1)设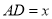 (
(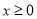 ),
), ,求用
,求用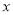 表示
表示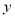 的函数关系式;
的函数关系式;
(2)如果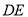 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,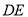 的位置应在哪里?如果
的位置应在哪里?如果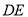 是参观线路,则希望它最长,
是参观线路,则希望它最长,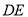 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com