
| 男 | 女 | |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
分析 (1)根据表中数据,计算老年人中需要志愿者提供帮助的老年人比例;
(2)补充2×2列联表,计算K2,与临界值比较得出概率结论.
解答 解:(1)根据表中数据知,估计该地区老年人中,需要志愿者提供帮助的老年人的比例为
$\frac{40+30}{40+30+160+270}$=0.14=14%;
(2)补充2×2列联表如下,
| 男 | 女 | 合计 | |
| 需要 | 40 | 30 | 70 |
| 不需要 | 160 | 270 | 430 |
| 合计 | 200 | 300 | 500 |
点评 本题考查了列联表与独立性检验的应用问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
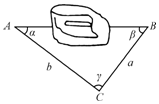 如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.
如图,某人为了测量某建筑物两侧A.B间的距离(在A,B处相互看不到对方),选定了一个可看到A、B两点的C点进行测量,你认为测量时应测量的数据是a,b,γ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $-\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com