
���� ��I��������ɵã�b=$\sqrt{3}$��$\frac{c}{a}=\frac{1}{2}$��a2=b2+c2��������ã�a��c�����ɵó���ԲC�ķ��̼��佹�࣮
��II����PA�ķ���Ϊ��my=x-2����m��0��������Բ����������Ϊ����3m2+4��y2+12my=0��
���P$��\frac{8-6{m}^{2}}{3{m}^{2}+4}��\frac{-12m}{3{m}^{2}+4}��$����B��2��t��������$\frac{t}{3}����\frac{1}{m}��$=-1�����t=-3m���ɵ�ֱ��BP�ķ���Ϊ��y+3m=kBP��x-2�����ɵ�ֱ��BP�������㣨-2��0����
��� �⣺��I��������ɵã�b=$\sqrt{3}$��$\frac{c}{a}=\frac{1}{2}$��a2=b2+c2��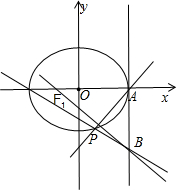
������ã�a=2��c=1��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1������Ϊ2��
��II����PA�ķ���Ϊ��my=x-2����m��0����
����$\left\{\begin{array}{l}{my=x-2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$��������3m2+4��y2+12my=0��
���yP=$\frac{-12m}{3{m}^{2}+4}$����xP=$\frac{8-6{m}^{2}}{3{m}^{2}+4}$��
��P$��\frac{8-6{m}^{2}}{3{m}^{2}+4}��\frac{-12m}{3{m}^{2}+4}��$��
��B��2��t������$\frac{t}{3}����\frac{1}{m}��$=-1�����t=-3m��
��ֱ��BP�ķ���Ϊ��y+3m=$\frac{-3m+\frac{12m}{3{m}^{2}+4}}{2-\frac{8-6{m}^{2}}{3{m}^{2}+4}}$��x-2����
����4y+m��6+3x��=0����6+3x=0��4y=0��
���x=-2��y=0��
��ֱ��BP�������㣨-2��0����
���� ���⿼������Բ�ı����̼������ʡ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�����ֱ��ֱ��б��֮��Ĺ�ϵ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
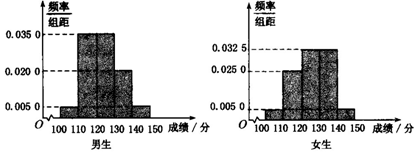
| ��ѧ������ | ��ѧ������ | �ϼ� | |
| ���� | |||
| �� | |||
| �ϼ� | 100 |
| ��P��K2��k2�� | 0.15�� | 0.10�� | 0.05�� | 0.025�� | 0.01�� | 0.005�� |
| ��k0 | 2.072�� | 2.706�� | 3.841�� | 5.024�� | 6.635�� | 7.879�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-5��-4�� | B�� | ��-5��0�� | C�� | ��-4��0�� | D�� | ��-5��-3] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | $\sqrt{2}$+$\frac{1}{2}$ | D�� | $\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 4 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | 2 | C�� | $2\sqrt{3}$ | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com