练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    不同三点A，B，C满足（
    BC
    •
    CA
    ）：（
    CA
    •
    AB
    ）：（
    AB
    •
    BC
    ）=3：4：5，则这三点（　　）
    A、组成锐角三角形
    B、组成直角三角形
    C、组成钝角三角形
    D、在同一条直线上
    考点：平面向量数量积的运算
    专题：解三角形,平面向量及应用
    分析：由条件可设三组数量积分别为，3m，4m，5m，然后观察三组数量积会发现，每两组数量积里都有相同的向量，对每两组数量积相加看出现什么情况，要判断三点共线，还是构成三角形，一般要看边的关系，若得出边的关系，本题答案可能就找到了．
    解答： 解：由题意设：
    BC
    •
    CA
    =3m，
    CA
    •
    AB
    =4m    ，
    AB
    •
    BC
    =5m    ，（m≠0）；
    BC
    •
    CA
    +
    CA
    •
    AB
    =
    CA
    (
    BC
    +
    AB
    )    =
    CA
    •
    AC
    =-(
    CA
    )2    =7m；
    CA
    •
    AB
    +
    AB
    •
    BC
    =
    AB
    (
    CA
    +
    BC
    )    =-(
    AB
    )2    =9m；
    AB
    •
    BC
    +
    BC
    •
    CA
    =-(
    BC
    )2=8m    ；所以，|
    CA
    |2=-7m，|
    AB
    |2=-9m    ，|
    BC
    |2=-8m
    显然，不存在两边之和等于第三遍的情况，故三点不在一条直线上，所以三点构成三角形，如下图，设A，B，C三点所对三边长分别为a，b，c，则由余弦定理得：cos∠ ACB=
    a2+b2-c2
    2ab
    =-
    32m
    		-7m
    		-8m
    ＞0    ，所以∠C是锐角，又∠C是最大边所对角，所以∠C最大，所以△ABC是锐角三角形．故答案选A．
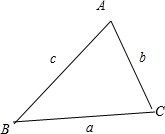
    点评：由比值的情况设出三组数量积的值，是解本题的关键，然后表示出了三边长度的平方，也就表示出了三边长度．而判断三点是否共线，只需说明两边之和是否等于第三边；而要判断是什么三角形，只需求出大边对的角的余弦值是大于0，等于0，还是小于0即可，这时需要应用余弦定理．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对于曲线y=ae
    b
    x
    ，令μ=lny，c=lna，v=
    1
    x
    ，可变换为线性回归模型，其形式为（　　）
    A、y=a+bv
    B、μ=a+bv
    C、μ=c+bv
    D、y=c+bx

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线C：
    y2
    a2
    -
    x2
    b2
    =1（a＞0，b＞0）的一条渐近方程为y=
    1
    2
    x，则C的离心率为（　　）
    A、
    		5
    2
    B、
    		5
    C、
    		3
    2
    D、
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列1，
    1
    2
    ，
    2
    2
    ，
    1
    3
    ，
    2
    3
    ，
    3
    3
    ，…，
    1
    n
    ，
    2
    n
    ，…，
    n
    n
    …的前18项的和（　　）
    A、11
    B、
    32
    3
    C、
    21
    2
    D、10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在R上的函数f（x），对任意x∈R，都有f（x+2）=-f（x）+f（1）成立，若函数y=f（x+1）的图象关于点（-1，0）对称，则f（2014）=（　　）
    A、3B、2014
    C、0D、-2014

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若A={x|-1＜x＜2}，B={x|1＜x＜3}，则A∩B=（　　）
    A、{x|1＜x＜2}
    B、{x|-1＜x＜3}
    C、{x|1＜x＜3}
    D、{x|-1＜x＜2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知一圆的方程式为x2+y2=v2t2，将该圆向下移动
    1
    2
    gt2个单位，求移动后圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}，{bn}满足a1=
    2
    3
    ，an+1=
    2an
    an+2
    ，b1+2b2+22b3+…+2n-1bn=n（n∈N*）．
    （1）求数列{an}和{bn}的通项公式；
    （2）设数列{
    bn
    an
    }的前n项和Tn，问是否存在正整数m、M且M-m=3，使得m＜Tn＜M对一切n∈N*恒成立？若存在，求出m、M的值；若不存在，请说明理由；
    （3）设cn=
    (anan+2)2
    an+1
    ，求证：c1+c2+c3+…+cn＜
    25
    72
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

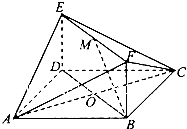    如图，已知正方形ABCD和矩形BDFE所在的平面互相垂直，AC交BD于O点，M为EF的中点，BC=
    		2
    ，BF=1
    （Ⅰ）求证：BC⊥AF：
    （Ⅱ）求证：BM∥平面ACE；
    （Ⅲ）求二面角B-AF-C的大小．

    查看答案和解析>>

    同步练习册答案