
分析 (1)根据降幂公式,化简得f(x)=$\frac{1}{2}$(b-a)cos2x+$\frac{1}{2}$(a+b),函数的值域为[1,3],列方程解得a=3,b=1,写出函数解析式,T=$\frac{2π}{ω}$;
(2)根据五点画出函数图象.
解答 解:(1)f(x)=asin2x+bcos2x(a>b),由降幂公式,可得:
f(x)=a•$\frac{1-cos2x}{2}$+b$\frac{1+cos2x}{2}$,
=$\frac{1}{2}$(b-a)cos2x+$\frac{1}{2}$(a+b),
函数f(x)的值域为[1,3],(a>b)
$\frac{1}{2}$(b-a)+$\frac{1}{2}$(a+b)=1,
-$\frac{1}{2}$(b-a)+$\frac{1}{2}$(a+b)=3,
解得:a=3,b=1,
∴f(x)=-cos2x+2,
T=$\frac{2π}{ω}$=$\frac{2π}{2}$=π,
f(x)的最小正周期π;
(2)函数在区间[-π,π]上的大致图象如图.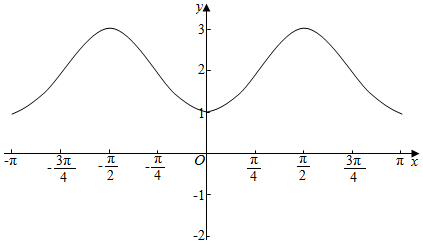
点评 本题考查降幂公式,求函数解析式,采用函数五点法,绘制函数解析式.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
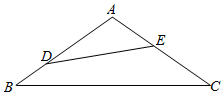 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 解:对于集合中最大的数a4,因为a4×a4>a4,3×a4>a4,2×a4>a4. 所以$\frac{a_4}{a_4}$,$\frac{a_4}{3}$,$\frac{a_4}{2}$都属于该集合. 又因为1≤a1<2<3<a4,所以$\frac{a_4}{a_4}<\frac{a_4}{3}<\frac{a_4}{2}<{a_4}$. 所以${a_1}=\frac{a_4}{a_4}=1$,$\frac{a_4}{3}=2,\frac{a_4}{2}=3$,故a1=1,a4=6. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com