练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．不等式x（1-x）＞0的解集为（　　）
    A．（-1，0）B．（-∞，-1）∪（0，+∞）C．（0，1）D．（-∞，0）∪（1，+∞）

    分析 由已知将不等式等价化为x（x-1）＜0，求出不等式的解集．

    解答 解：由已知，不等式等价于x（x-1）＜0，所以不等式的解集为：{x|0＜x＜1}；
    故选C．

    点评 本题考查了一元二次不等式的解法；等价将不等式化为二次项系数为正数，然后根据二次不等式与二次函数的关系，求出不等式的解集．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．已知平面向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（x-1，2），若$\overrightarrow{a}$与$\overrightarrow{b}$共线且方向相同，则x=（　　）
    A．1B．2C．-1D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．△ABC的内角A，B，C所对的边分别为a，b，c，若A，B，C形成等差数列．
    （1）求cosB的值；
    （2）若b=$\sqrt{7}$，a=2，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如图是一个几何体的三视图，则该几何体的表面积为（　　）
    A．46B．48C．50D．52

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列函数中，既是偶函数又在区间 （0，+∞）上单调递减的是（　　）
    A．y=$\frac{1}{x}$B．y=e-xC．y=-x2+1D．y═lg|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．实数a，b，c满足a+b+c=3，ab+2c=6，则实数c的取值范围是（　　）
    A．（-∞，-5]∪[3，+∞）B．[-5，3]C．（-∞，-3]∪[5，+∞）D．[-3，5]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知曲线C1：y=sinx，C2：y=sin（2x+$\frac{2π}{3}$），则下面结论正确的是（　　）
    A．把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变，再把得到的曲线向左平移$\frac{2π}{3}$个单位长度，得到曲线C2
    B．把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变，再把得到的曲线向左平移$\frac{π}{3}$个单位长度，得到曲线C2
    C．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移$\frac{2π}{3}$个单位长度，得到曲线C2
    D．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个$\frac{π}{3}$单位长度，得到曲线C2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若变量x，y满足$\left\{\begin{array}{l}{x+y≤2}\\{2x-3y≤9}\\{x≥0}\end{array}\right.$，则2x-y的最大值是（　　）
    A．-2B．3C．7D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

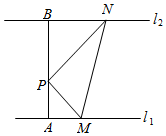    7．如图，P是两条平行直线l1，l2之间的一个定点，且点P到l1，l2的距离分别为PA=1，PB=$\sqrt{3}$，设△PMN的另两个顶点M，N分别在l1，l2上运动，设∠MPN=α，∠PMN=β，∠PNM=γ，且满足sinβ+sinγ=sinα（cosβ+cosγ）．
    （Ⅰ）求α；
    （Ⅱ）求$\frac{1}{PM}$+$\frac{\sqrt{3}}{PN}$的最大值．

    查看答案和解析>>

    同步练习册答案