
分析 以等腰梯形ABCD的底AB所在的直线为x轴,以AB的垂直平行线为y轴,建立如图所示的坐标系,根据向量的坐标运算求出$\overrightarrow{AE}$,$\overrightarrow{DF}$,
(1)当λ=$\frac{1}{2}$时,$\overrightarrow{AE}$=($\frac{7}{4}$,$\frac{\sqrt{3}}{4}$),即可求出答案,
(2)根据向量的数量积和基本不等式即可求出答案.
解答 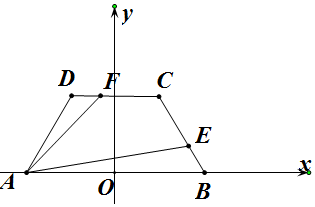 解:以等腰梯形ABCD的底AB所在的直线为x轴,以AB的垂直平分线为y轴,建立如图所示的坐标系,
解:以等腰梯形ABCD的底AB所在的直线为x轴,以AB的垂直平分线为y轴,建立如图所示的坐标系,
∵AB∥DC,AB=2,BC=1,∠ABC=60°,
∴A(-1,0),B(1,0),C($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
D(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=(2,0)+λ(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)
=(2-$\frac{1}{2}$λ,$\frac{\sqrt{3}}{2}$λ),
(1)当λ=$\frac{1}{2}$时,$\overrightarrow{AE}$=($\frac{7}{4}$,$\frac{\sqrt{3}}{4}$),则|$\overrightarrow{AE}$|=$\sqrt{\frac{49}{16}+\frac{3}{16}}$=$\frac{\sqrt{13}}{2}$
(2)∵$\overrightarrow{DE}$=$\overrightarrow{AD}$+$\overrightarrow{DF}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)+$\frac{1}{9λ}$(1,0)=($\frac{1}{2}$+$\frac{1}{9λ}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AE}•\overrightarrow{AF}$=$\frac{17}{18}$+$\frac{2}{9λ}$+$\frac{λ}{2}$≥$\frac{17}{18}$+2$\sqrt{\frac{2}{9λ}•\frac{λ}{2}}$=$\frac{17}{18}$+$\frac{2}{3}$=$\frac{29}{18}$,当且仅当λ=$\frac{2}{3}$时取得最小值.
点评 本题考查了等腰梯形的性质以及向量的数量积公式的运用、基本不等式求最值;关键是正确表示所求,利用基本不等式求最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{4}{3}$,1) | B. | ($\frac{4}{3}$,2) | C. | (1,$\frac{4}{3}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com