练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    长方体ABCD-A1B1C1D1中，已知二面角A1-BD-A的大小为
    π
    6
    ，若空间有一条直线l与直线CC1，所成的角为
    π
    4
    ，则直线l与平面A1BD所成角的取值范围是（　　）
    A、[
    π
    12
    ，
    7π
    12
    ]
    B、[
    π
    12
    ，
    π
    2
    ]
    C、[
    π
    12
    ，
    5π
    12
    ]
    D、[0，
    π
    2
    ]
    考点：直线与平面所成的角
    专题：空间位置关系与距离
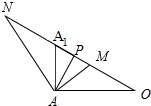
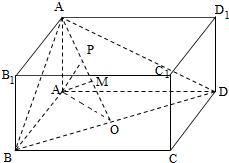
    分析：如图所示，过点A作AO⊥BD，连接A1O，由三垂线定理可得BD⊥A1O，则∠AOA1为二面角A1-BD-A的平面角．把直线l平移到AM，则∠A1AM=∠MAO=
    π
    4
    ．过点A作AP⊥A1O，则AP⊥平面A1BD．利用线面角的定义可得：AM（即直线l）与平面A1BD所成的最大角为∠AMA1．假设∠A1AN=
    π
    4
    ，AN与直线OP相交于点N，则AN（即直线l）与平面A1BD所成的最小角为∠ANP．
    解答： 解：如图所示，过点A作AO⊥BD，连接A1O，由三垂线定理可得BD⊥A1O，则∠AOA1为二面角A1-BD-A的平面角，∴∠AOA1=
    π
    6
    ．
    把直线l平移到AM，则∠A1AM=∠MAO=
    π
    4
    ．
    过点A作AP⊥A1O，则AP⊥平面A1BD．
    ∴AM（即直线l）与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=
    π
    4
    +
    π
    6
    =
    5π
    12
    ．
    假设∠A1AN=
    π
    4
    ，AN与直线OP相交于点N，则AN（即直线l）与平面A1BD所成的最小角为
    ∠ANP=∠PA1A-∠A1AN=
    π
    3
    -
    π
    4
    =
    π
    12
    ．
    ∴直线l与平面A1BD所成角的取值范围是[
    π
    12
    ，
    5π
    12
    ]    ．
    故选：C．
    点评：本题考查了二面角的平面角、线面角、三垂线定理、异面直线所成的角，考查了空间想象能力，考查了推理能力与计算能力，属于难题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    计算：
    （1）cos（-
    79
    6
    π）
    （2）sin（α+180°）cos（-α）sin（-α-180°）
    （3）cos（-
    π
    6
    ）
    （4）sin（-
    5
    3
    π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，A，B，C所对边的长分别为a，b，c，已知b=
    		7
    ，c=2，B=
    π
    3
    ，则a=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    位于坐标原点的一个支点P按下述规则移动：质点每次移动一个单位：移动的方向为向上或向右，并且向上、向右移动的概率都是0.5，质点P移动6次后位于点（2，4）的概率为（　　）
    A、（
    1
    2
    ）6
    B、C
     
    2
    6
    （
    1
    2
    ）6
    C、C
     
    2
    6
    （
    1
    2
    ）2
    D、C
     
    2
    6
    C
     
    4
    6
    （
    1
    2
    ）6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的函数f（x）满足f（-x）+f（x）且周期是4，若f（1）=5，则f（2015）（　　）
    A、5B、-5C、0D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直线y=k（x+4）与曲线x=
    		4-y2
    有交点，则k的取值范围是（　　）
    A、[-
    1
    2
    ，
    1
    2
    ]
    B、（-∞，-
    1
    2
    ）∪（
    1
    2
    ，+∞）
    C、[-
    		3
    3
    ，
    		3
    3
    ]
    D、（-∞，-
    		3
    3
    ]∪[
    		3
    3
    ，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}为等比数列，且a1+a2=3，a4+a5=24
    （1）求数列{an}的通项公式；
    （2）令bn=log2an+1，设{
    1
    bnbn+1
    }    的前n项和为Sn，若Sn=
    2014
    2015
    ，求n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    三个变量y1，y2，y3随x的变化情况如下表：
    x1.003.005.007.009.0011.00
    y15135625171536456655
    y2529245218919685177149
    y35.006.106.616.957.207.40
    三个变量y1，y2，y3中，变量
     
    随x呈对数函数型变化，变量
     
    随x呈指数函数型变化，变量
     
    随x呈幂函数变化．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cos（
    π
    4
    -a）=
    3
    5
    ，-
    3π
    2
    ＜α＜-
    π
    2
    ，求cos（2α-
    π
    4
    ）的值．

    查看答案和解析>>

    同步练习册答案