
���� ��1������������ɵ�an+1-an=1�����ɵȲ����еĶ����ͨ�ʽ�����ɵõ�����
��2�����${b_n}={2^n}•��n+1��$���������е���ͷ�������λ���������ϵȱ����е����ʽ�����㼴�ɵõ�����ͣ�
��3�����an=n+1��${C_n}={4^n}-��•{2^{n+1}}$��ҪʹCn+1��Cn�������������������ɲ������룬����ұߵ���Сֵ���ɵõ�����Χ��
��� �⣺��1������֪�ɵã�$��{a_{n+1}}+{a_n}��•��{a_{n+1}}-{a_n}��=��{a_{n+1}}+{a_n}����n��{N^*}��$����an��0��
��an+1-an=1��n��N*������a2-a1=1��
������{an}����a1=2Ϊ�������Ϊ1�ĵȲ����У�
��an=n+1��
��2���ɣ�1��֪${b_n}={2^n}•��n+1��$��
������ǰn���ΪTn
��Tn=2•21+3•22+��+��n+1��•2n��
2Tn=2•22+3•23+��+��n+1��•2n+1��
��ʽ����ɵã�$-{T_n}=2��{2^1}+{2^2}+{2^3}+��+{2^{n-1}}+{2^n}-��n+1����{2^{n+1}}=-n•{2^{n+1}}$
����${T_n}=n•{2^{n+1}}$��
��3����an=n+1����${C_n}={4^n}-��•{2^{n+1}}$��
ҪʹCn+1��Cn�������
��${C_{n+1}}-{C_n}={4^{n+1}}-{4^n}-��•{2^{n+2}}+��•{2^{n+1}}��0$�������
��3•4n-��•2n+1��0�������
��ˣ�3•2n-1�������
���ҽ���n=1ʱ��3•2n-1����СֵΪ3����ˣ�3���֦�Ϊ��ż�������=2��
�����ڦ�=2��ʹ�ö�����n��N*������Cn+1��Cn��
���� ���⿼�����е�ͨ�ʽ����ע�����õȲ����еĶ����ͨ�ʽ���������е���ͷ�������λ�������ͬʱ������������Ľⷨ��ע���������еĵ����ԣ����黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{\sqrt{6}+2}{4}$ | C�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | D�� | $\frac{\sqrt{2}+2}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��6 | B�� | 0��8 | C�� | 2��0 | D�� | 6��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{{-1��\frac{1}{2}}\right\}$ | B�� | {-1��0} | C�� | $\left\{{-1��0��\frac{1}{2}}\right\}$ | D�� | $\left\{{0��\frac{1}{2}}\right\}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
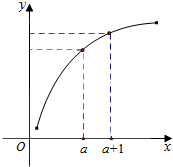
| A�� | 0��f�䣨a����f�䣨a+1����f��a+1��-f��a�� | B�� | 0��f�䣨a+1����f��a+1��-f��a����f�䣨a�� | ||
| C�� | 0��f�䣨a+1����f�䣨a����f��a+1��-f��a�� | D�� | 0��f��a+1��-f��a����f�䣨a����f�䣨a+1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
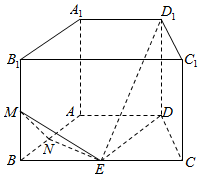 ��ͼ��ֱ������ABCD-A1B1C1D1�ĵ����ǵ������Σ�AB=CD=AD=1��BC=2��E��M��N�ֱ�����������е㣮
��ͼ��ֱ������ABCD-A1B1C1D1�ĵ����ǵ������Σ�AB=CD=AD=1��BC=2��E��M��N�ֱ�����������е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com