
分析 根据函数图象平移变换法则,可判断①;判断x∈(0,1)时,x$-\frac{1}{x}$的范围,可判断②;根据充要条件的定义,可判断③;根据正弦型函数的对称性和奇偶性,可判断④.
解答 解:①函数$f(x)=\frac{2x-1}{x+1}$=$\frac{-3}{x+1}$+2,其图象由反比例函数y=$\frac{-3}{x}$的图象向左平移两单位,再向上平移2个单位得到,故图象的对称中心是(-1,2),故①正确;
②x∈(0,1)时,x$-\frac{1}{x}$∈(-∞,0),若关于x的方程$x-\frac{1}{x}+k=0在x∈({0,1})$没有实数根,则k的取值范围是k≥0,故②错误;
③在△ABC中,“bcosA=acosB”?“sinBcosA=sinAcosB”?“sin(A-B)=0”?“A=B”⇒“△ABC为等腰三角形”,“bcosA=acosB”是“△ABC为等边三角形”的必要不充分条件,故③错误;
④若$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移φ(φ>0)个单位后为奇函数,-2φ-$\frac{π}{3}$=kπ,k∈Z,
当k=-1时,φ最小值是$\frac{π}{3}$,故④错误;
故答案为:①
点评 本题以命题的真假判断与应用为载体,考查了函数的对称性,方程的根,函数的值域,充要条件,正弦型函数的图象和性质,难度中档.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
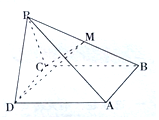 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,2] | B. | ($\frac{3}{2}$,2) | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com