



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| f(x) |
| x+1 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
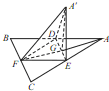 ИзНјЈ¬±Яі¤ОЄaµДµИ±ЯИэЅЗРОABCµДЦРПЯAFУлЦРО»ПЯDEЅ»УЪµгGЈ¬ТСЦЄЎчAЎдDEЈЁAЎд∉ЖЅГжABCЈ©КЗЎчADEИЖDEРэЧЄ№эіМЦРµДТ»ёцНјРОЈ¬УРПВБРГьМвЈє
ИзНјЈ¬±Яі¤ОЄaµДµИ±ЯИэЅЗРОABCµДЦРПЯAFУлЦРО»ПЯDEЅ»УЪµгGЈ¬ТСЦЄЎчAЎдDEЈЁAЎд∉ЖЅГжABCЈ©КЗЎчADEИЖDEРэЧЄ№эіМЦРµДТ»ёцНјРОЈ¬УРПВБРГьМвЈє| 1 |
| 64 |
| ¦Р |
| 2 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| 2-sinx |
| 2+sinx |
| ||
| 2 |
5
| ||
| 8 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
|
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
|
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| ¦Р |
| 3 |
AЎў
| ||||
BЎў-
| ||||
CЎў
| ||||
DЎў-
|
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| 1 |
| 12 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 11 |
| 18 |
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com