
| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出AB′与A′C′所在直线的夹角.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A′B′C′D′中棱长为1,
则A(1,0,0),B′(1,1,1),A′(1,0,1),C′(0,1,1),
$\overrightarrow{A{B}^{'}}$=(0,1,1),$\overrightarrow{{A}^{'}{C}^{'}}$=(-1,1,0),
设AB′与A′C′所在直线的夹角为θ,
则cosθ=$\frac{|\overrightarrow{A{B}^{'}}•\overrightarrow{{A}^{'}{C}^{'}}|}{|\overrightarrow{A{B}^{'}}|•|\overrightarrow{{A}^{'}{C}^{'}}|}$=$\frac{1}{\sqrt{2}×\sqrt{2}}$=$\frac{1}{2}$,
∴AB′与A′C′所在直线的夹角为60°.
故选:B.
点评 本题考查两条异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 蒙特卡洛方法的思想如下:当所求解的问题是某种随机事件=出现的概率时,通过某种“试验”方法,以这种事件出现的频率估计这一随机事件的概率,并将其作为问题的解.现为了估计右图所示的阴影部分面积的大小,使用蒙特卡洛方法的思想,向面积为16的矩形OABC内投掷800个点,其中恰有180个点落在阴影部分内,则可估计阴影部分的面积为( )
蒙特卡洛方法的思想如下:当所求解的问题是某种随机事件=出现的概率时,通过某种“试验”方法,以这种事件出现的频率估计这一随机事件的概率,并将其作为问题的解.现为了估计右图所示的阴影部分面积的大小,使用蒙特卡洛方法的思想,向面积为16的矩形OABC内投掷800个点,其中恰有180个点落在阴影部分内,则可估计阴影部分的面积为( )| A. | 3.6 | B. | 4 | C. | 12.4 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+{y^2}$=1 | B. | $\frac{y^2}{4}+{x^2}$=1 | ||
| C. | $\frac{x^2}{4}+{y^2}$=1或$\frac{y^2}{4}+{x^2}$=1 | D. | $\frac{y^2}{4}+\frac{x^2}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
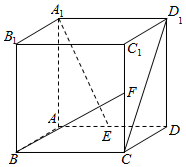 如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.
如图,设正方形ABCD-A1B1C1D1的棱长为2,E、F分别是AD和CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com