
| x | -8 | -4 | 3 | 5 |
| y | 19 | 7 | -3 | -9 |
分析 求出样本中心坐标,代入回归方程求出$\stackrel{∧}{a}$.
解答 解:$\overline{x}$=$\frac{-8+(-4)+3+5}{4}$=-1,$\overline{y}$=$\frac{19+7+(-3)+(-9)}{4}$=3.5,
由回归直线方程过样本中心点($\overline{x}$,$\overline{y}$)即(-1,3.5),
则$\stackrel{∧}{a}$=$\overline{y}$+2$\overline{x}$=3.5-2=1.5,
故答案为:1.5.
点评 本题考查了线性回归直线的性质,回归直线必过样本的中心点,属于基础题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
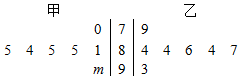
| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | D. | $\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{2}$] | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{6}$] | D. | [$\frac{π}{6}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
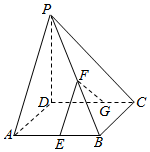 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为正方形,PD=DC=2,E、F、G分别是AB、PB、CD的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD为正方形,PD=DC=2,E、F、G分别是AB、PB、CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 角B是锐角 | B. | 角B不是锐角 | C. | 角B是直角 | D. | 角B是钝角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com