
分析 (1)利用椭圆的性质得到c,求出a,b,即可求解椭圆方程.
(2)设M(x1,y1)N(x2,y2),联立直线与椭圆方程,利用判别式以及韦达定理,求出MN的中点坐标,利用AM=AN,验证m是否存在即可.
解答 解:(1)因为焦点在x轴,顶点A(0,-1),∴b=1,设右焦点坐标为(c,0),
由题意得$\frac{{|{c+2\sqrt{2}}|}}{{\sqrt{2}}}=3$,∴$c=\sqrt{2}$,
可得b=1,
∴$\frac{x^2}{3}+\frac{y^2}{1}=1$;
(2)设M(x1,y1)N(x2,y2),$\left\{{\begin{array}{l}{y=x+m}\\{{x^2}+3{y^2}-3=0}\end{array},4{x^2}+6mx+3{m^2}-3=0,\left\{{\begin{array}{l}{△=36{m^2}-16({3{m^2}-3})>0}\\{{x_1}+{x_2}=-\frac{3m}{2}}\end{array}}\right.}\right.$,
即M,N的中点坐标$Q({-\frac{3m}{4},\frac{m}{4}})$,∵AM=AN,
∴kAQ=-1,∴m=2经检验△=0不合题意,
∴不存在.
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,考查转化思想以及计算能力.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},+∞)$ | B. | $(-∞,\frac{1}{2})$ | C. | $({\frac{1}{2},2}]$ | D. | $[{-2,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
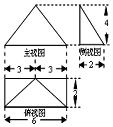
| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com