
【题目】对于函数f(x),若f(x0)=x0,则称x0为f(x)的不动点.设f(x)=x3+ax2+bx+3.
(1)当a=0时,
(i)求f(x)的极值点;
(ⅱ)若存在x0既是f(x)的极值点,也是f(x)的不动点,求b的值;
(2)是否存在a,b,使得f(x)有两个极值点,且这两个极值点均为f(x)的不动点?说明理由.
【答案】(1)(i)![]() 是f(x)的极大值点,
是f(x)的极大值点,![]() 是f(x)的极小值点(ⅱ)b=﹣3(2)不存在满足题设的a,b;详见解析
是f(x)的极小值点(ⅱ)b=﹣3(2)不存在满足题设的a,b;详见解析
【解析】
(1)(i)求出导数![]() ,由
,由![]() 的根确定函数的单调性,从而确定极值点.
的根确定函数的单调性,从而确定极值点.
(ⅱ)由![]() 和
和![]() 结合可解得
结合可解得![]() ;
;
(2)假设存在![]() 满足题意,由函数的单调性和不动点定义可得矛盾,说明假设错误.
满足题意,由函数的单调性和不动点定义可得矛盾,说明假设错误.
(1)当a=0时,f(x)=x3+bx+3,f′(x)=3x2+b,
(i)①当b≥0,f(x)在R单调递增,无极值点,
②当b<0时,由f′(x)=0,得![]() 或
或![]() ,
,
当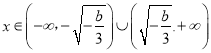 ,f′(x)>0,故f(x)在
,f′(x)>0,故f(x)在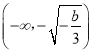 ,
,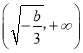 单调递增,
单调递增,
当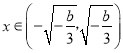 时,f′(x)<0,
时,f′(x)<0,
在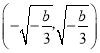 单调递减,
单调递减,
所以,![]() 是f(x)的极大值点,
是f(x)的极大值点,![]() 是f(x)的极小值点.
是f(x)的极小值点.
(ⅱ)设x=x0是f(x)的极值点,则由(i)可知![]() ,
,
又x=x0是f(x)的不动点,则![]() ,
,
所以b=﹣3,
(2)不存在满足题设的a,b,
证明如下:
假设存在满足题设的a,b,设x1,x2为f(x)的两个极值点,且为f(x)的不动点,并不妨设x1<x2,
由于f′(x)=3x2+2ax+b,
所以x1,x2为方程3x2+2ax+b=0的两个根,
当x∈(x1,x2)时,f′(x)<0,可知f(x)在(x1,x2)上单调递减,故f(x1)>f(x2),
又x1,x2为f(x)的不动点,所以f(x1)=x1<x2=f(x2),
即f(x1)<f(x2),矛盾,
所以不存在满足题设的a,b.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分.每项评分最低分0分,最高分100分.每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如图
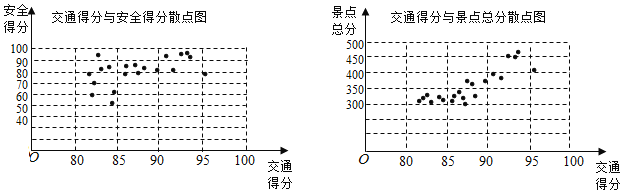
请根据图中所提供的信息,完成下列问题:
(1)若从交通得分排名前5名的景点中任取1个,求其安全得分大于90分的概率;
(2)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为ξ,求随机变量ξ的分布列和数学期望;
(3)记该市26个景点的交通平均得分为![]() ,安全平均得分为
,安全平均得分为![]() ,写出
,写出![]() 和
和![]() 的大小关系?(只写出结果)
的大小关系?(只写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求实数
,若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的![]() .则第二名选手的得分是____.
.则第二名选手的得分是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD中,∠BAD=60°,AC与BD相交于点O.将△ABD沿BD折起,使顶点A至点M,在折起的过程中,下列结论正确的是( )
A.BD⊥CM
B.存在一个位置,使△CDM为等边三角形
C.DM与BC不可能垂直
D.直线DM与平面BCD所成的角的最大值为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com