
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
分析 对等式$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$两边分别乘以$\overrightarrow{AB}$,$\overrightarrow{AC}$便可得到$\left\{\begin{array}{l}{\overrightarrow{AO}•\overrightarrow{AB}=x{\overrightarrow{AB}}^{2}+y\overrightarrow{AB}•\overrightarrow{AC}}\\{\overrightarrow{AO}•\overrightarrow{AC}=x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}}\end{array}\right.$,根据O为△ABC外接圆的圆心,便可得到$\overrightarrow{AO}•\overrightarrow{AB}=\frac{9}{2},\overrightarrow{AO}•\overrightarrow{AC}=8$,从而可以得出$\left\{\begin{array}{l}{\frac{9}{2}=9x+12ycos∠BAC}\\{8=12xcos∠BAC+16y}\end{array}\right.$,然后联立x+2y=1即可解出x,y,cos∠BAC,并需满足x,y非零,这便可得出cos∠BAC.
解答 解:如图,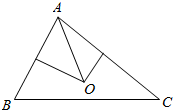
由$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$得:
$\left\{\begin{array}{l}{\overrightarrow{AO}•\overrightarrow{AB}=x{\overrightarrow{AB}}^{2}+y\overrightarrow{AB}•\overrightarrow{AC}}\\{\overrightarrow{AO}•\overrightarrow{AC}=x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}}\end{array}\right.$;
$\overrightarrow{AO}•\overrightarrow{AB}=|\overrightarrow{AO}||\overrightarrow{AB}|•\frac{\frac{1}{2}|\overrightarrow{AB}|}{|\overrightarrow{AO}|}=\frac{9}{2}$,$\overrightarrow{AO}•\overrightarrow{AC}=|\overrightarrow{AO}||\overrightarrow{AC}|$$•\frac{\frac{1}{2}|\overrightarrow{AC}|}{|\overrightarrow{AO}|}$=8;
∴$\left\{\begin{array}{l}{\frac{9}{2}=9x+12ycos∠BAC}\\{8=12xcos∠BAC+16y}\end{array}\right.$,联立x+2y=1解得,$\left\{\begin{array}{l}{x=\frac{1}{10}}\\{y=\frac{9}{20}}\\{cos∠BAC=\frac{2}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=\frac{1}{2}}\\{cos∠BAC=\frac{3}{4}}\end{array}\right.$;
∵x,y都不为0;
∴$cos∠BAC=\frac{2}{3}$.
故选:A.
点评 考查向量数量积的运算及其计算公式,三角形外接圆圆心的概念,余弦函数的定义,能够通过联立三个方程解出三元二次方程组.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
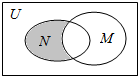 设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )| A. | {x|x<2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{9}{2}$ | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10种 | B. | 20种 | C. | 40种 | D. | 80种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com