
分析 (1)由CC1∥BB1,得∠A1B1B是A1B1与C1C所成的角,由此能求出A1B1与C1C所成的角.
(2)由AD∥BC,得∠B1BC是AD与B1B所成的角,由此能求出AD与B1B所成的角.
(3)由A1D∥B1C,B1C⊥BC1,能求出A1D与BC1所成的角;
(4)由D1C∥A1B,得∠AA1B是D1C与A1A所成的角,由此能求出D1C与A1A所成的角;
(5)由A1D∥B1C,得∠B1CA是A1D与AC所成的角,由此能求出A1D与AC所成的角.
解答 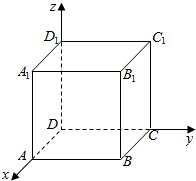 解:(1)正方体ABCD-A1B1C1D1中,
解:(1)正方体ABCD-A1B1C1D1中,
∵CC1∥BB1,∴∠A1B1B是A1B1与C1C所成的角,
∵A1B1⊥BB1,∴∠A1B1B=90°,
∴A1B1与C1C所成的角为90°.
(2)∵AD∥BC,∴∠B1BC是AD与B1B所成的角,
∵BB1⊥BC,∴∠B1BC=90°,
∴AD与B1B所成的角为90°.
(3)∵A1D∥B1C,又B1C⊥BC1,
∴A1D与BC1所成的角为90°;
(4)∵D1C∥A1B,∴∠AA1B是D1C与A1A所成的角,
∵AA1=AB,AA1⊥AB,
∴∠AA1B=45°,
∴D1C与A1A所成的角为45°;
(5)∵A1D∥B1C,∴∠B1CA是A1D与AC所成的角,
∵B1C=AC=AB1,∴∠B1CA=60°,
∴A1D与AC所成的角为60°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
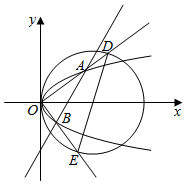 如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )
如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
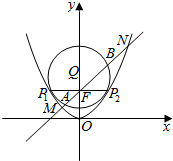 如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.
如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
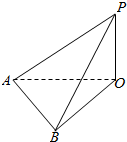 如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.
如图所示,在地面上有一旗杆OP,测得它的高度10m,在地面上取一基线AB,AB=20m,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,则∠AOB=$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
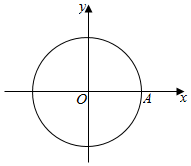 如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.
如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com