
分析 由题意f(x)为R上偶函数,f(x)=x3 在x>0上为单调增函数知|3x-t|≥|2x|,转化为对任意x∈[2t-1,2t+3],5x2-6xt+t2≥0 恒成立问题.
解答 解:f(x)为R上偶函数,f(x)=x3 在x>0上为单调增函数,
f(3x-t)≥8f(x)=f(2x);
|3x-t|≥|2x|;
∴(3x-t)2≥(2x)2;
化简后:5x2-6xt+t2≥0 ①;
(1)当t>0时,①式解为:x≤$\frac{t}{5}$或 x≥t;
对任意x∈[2t-1,2t+3],①式恒成立,则需:t≤2t-1
故t≥1;
(2)当t<0时,①是解为:x≤t 或 x≥$\frac{t}{5}$;
对任意x∈[2t-1,2t+3],①式恒成立,则需:2t+3≤t
故t≤-3;
(3)当t=0时,①式恒成立;
综上所述,t≤-3或t≥1或t=0.
故答案为t≤-3或t≥1或t=0.
点评 本题主要考查了函数的基本性质,以及函数恒成立问题,属中等题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
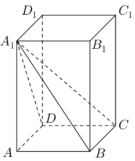 如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;
如图,长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=3;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $3+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在$(0,\frac{π}{2})$单调递减 | B. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递减 | ||
| C. | f(x)在$(0,\frac{π}{2})$单调递增 | D. | f(x)在$(\frac{π}{4},\frac{3π}{4})$单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com