
分析 (1)由题意得数列{an}是以2为公比、首项a1=2的等比数列,数列{bn}是以2为公差、首项b1=1的等差数列,进而得到答案;
(2)利用放缩法,结合裂项相消法,可得$\frac{1}{B_1}+\frac{1}{B_2}+…+\frac{1}{B_n}$<2;
(3)利用错位相减法,求出${T_n}=3-\frac{1}{{{2^{n-2}}}}-\frac{2n-1}{2^n}<3$,可得结论.
解答 解:(1)由题意得2an=Sn+2,即2a1=S1+2=a1+2,
所以a1=2
因为Sn=2an-2,Sn+1=2an+1-2,
所以an+1=Sn+1-Sn=2(an+1-an),即an+1=2an,
所以数列{an}是以2为公比、首项a1=2的等比数列,
即${a_n}={2^n}({n∈N*})$
因为点P(bn,bn+1)在直线y=x+2上,
所以bn+1=bn+2,即bn+1-bn=2,
所以数列{bn}是以2为公差、首项b1=1的等差数列,
即bn=2n-1(n∈N*)…(4分)
(2)${B_n}={b_1}+{b_2}+…+{b_n}={n^2}$,
所以
$\begin{array}{l}\frac{1}{B_1}+\frac{1}{B_2}+…+\frac{1}{B_n}=\frac{1}{1^2}+\frac{1}{2^2}+…+\frac{1}{n^2}<1+\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{(n-1)×n}\\=1+(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n-1}-\frac{1}{n})=2-\frac{1}{n}<2\end{array}$…(8分)
(3)因为${T_n}=\frac{b_1}{a_1}+\frac{b_2}{a_2}+…+\frac{b_n}{a_n}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$①
所以$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{3}{2^3}+…+\frac{2n-1}{{{2^{n+1}}}}$②
①-②得$\frac{1}{2}{T_n}=\frac{1}{2}+2(\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n})-\frac{2n-1}{{{2^{n+1}}}}=\frac{1}{2}+2×\frac{{\frac{1}{4}×(1-\frac{1}{{{2^{n-1}}}})}}{{1-\frac{1}{2}}}-\frac{2n-1}{{{2^{n+1}}}}$
所以${T_n}=3-\frac{1}{{{2^{n-2}}}}-\frac{2n-1}{2^n}<3$
又由${T_1}=\frac{1}{2}$,Tn单调递增,
所以${T_n}∈[{\frac{1}{2},3})$…(12分)
点评 本题考查的知识点是等差数列和等比数列,数列求和,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
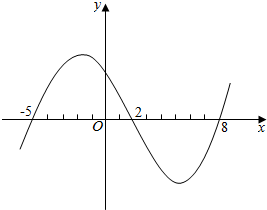
| A. | f(-2)>f(1) | B. | f(-2)<f(1) | ||
| C. | f(-2)=f(1) | D. | f(-2)与f(1)的大小不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -6 | C. | 2或-8 | D. | 2或-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com