
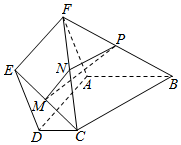
 如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.
如图,已知四边形ADEF为矩形,四边形ABCD为直角梯形且AB⊥AD,AB∥CD,M、N、P分别为EC、FC、FB的中点.分析 (Ⅰ)运用三角形的中位线定理,运用线面平行的判定定理,可得平面MNP∥平面ABCD,再由性质定理即可得证;
(Ⅱ)运用矩形的定义和直角梯形的定义,结合线面垂直的判定定理,可得MN⊥平面ECD,再由面面垂直的判定定理,即可得证.
解答 证明:(Ⅰ)由M,N分别为EC,FC的中点,可得
MN∥EF,又EF∥AD,即有MN∥AD,
MN?平面ABCD,AD?平面ABCD,
可得MN∥平面ABCD;
同理可得NP∥平面ABCD,
又MN∩NP=N,且MN,NP?平面MNP,
可得平面MNP∥平面ABCD,
由MP?平面MNP,
可得MP∥平面ABCD;
(Ⅱ)由矩形ADEF可得AD⊥DE,
由ABCD为直角梯形,且AB⊥AD,
可得AD⊥DC,
即有AD⊥平面ECD,
由AD∥MN,可得MN⊥平面ECD,
由MN?平面MNP,可得
平面MNP⊥平面EDC.
点评 本题考查线面平行的判定,注意运用面面平行的性质定理,考查面面垂直的判定,注意运用判定定理,同时考查线面和面面位置关系的转化思想的运用,考查空间想象能力和逻辑推理的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | {0,1} | C. | {(0,1)} | D. | {(0,0),(1,1)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {2,4} | C. | {2,6} | D. | {6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 试销价格x(元) | 4 | 5 | 6 | 7 | a | 9 |
| 产品销量y(件) | b | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com