Question

已知三角形的三边为a，b，c，设p=

1

2

（a+b+c），求证：
（1）三角形的面积S=

p(p-a)(p-b)(p-c)

．
（2）r为三角形内切圆的半径，则r=

(p-a)(p-b)(p-c) p

．
（3）把边BC，CA，AB上的高分别记为h_a，h_b，h_c，则．
h_a=

2

a

p(p-a)(p-b)(p-c)

，h_b=

2

b

p(p-a)(p-b)(p-c)

，h_c=

2

c

p(p-a)(p-b)(p-c)

．

Answer 1

考点：余弦定理,正弦定理

专题：计算题,解三角形

分析：（1）设三角形的三边a、b、c的对角分别为A、B、C，则由余弦定理可得cosC=

a2+b2-c2

2ab

，代入三角形面积公式S=

1

2

absinC，设p=

a+b+c

2

，则p-a=

-a+b+c

2

，p-b=

a-b+c

2

，p-c=

a+b-c

2

，即可化简得证．
（2）由（1）可得S=

p(p-a)(p-b)(p-c)

．而又因为S=

r(a+b+c)

2

，结合上述两式即可得证．
（3）由三角形面积公式可得S=

p(p-a)(p-b)(p-c)

=

1

2

ah_a=

1

2

bh_b=

1

2

ch_c，即可得解．

解答： 解：（1）设三角形的三边a、b、c的对角分别为A、B、C，则由余弦定理可得：
cosC=

a2+b2-c2

2ab

，
S=

1

2

absinC
=

1

2

ab

1-cos2C

=

1

2

ab

1- (a2+b2-c2)2 4a2b2

=

1

4

4a2b2-(a2+b2-c2)2

=

1

4

(2ab+a2+b2-c2)(2ab-a2-b2+c2)

=

1

4

[(a+b)2-c2][c2-(a-b)2]

=

1

4

(a+b+c)(a+b-c)(a-b+c)(-a+b+c)

，①
设p=

a+b+c

2

，
则p-a=

-a+b+c

2

，p-b=

a-b+c

2

，p-c=

a+b-c

2

，
上式①=

(a+b+c)(a+b-c)(a-b+c)(-a+b+c) 16

=

p(p-a)(p-b)(p-c)

．
所以，三角形的面积S=

p(p-a)(p-b)(p-c)

．
（2）根据海伦公式：三角形的面积S=

p(p-a)(p-b)(p-c)

．
而又因为S=

1

2

ar+

1

2

br+

1

2

cr=

r(a+b+c)

2

（如下图所示），

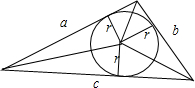
结合上述两式：r=

(p-a)(p-b)(p-c) p

，证毕．
（3）∵边BC，CA，AB上的高分别记为h_a，h_b，h_c，三角形的面积S=

p(p-a)(p-b)(p-c)

．
∴S=

p(p-a)(p-b)(p-c)

=

1

2

ah_a=

1

2

bh_b=

1

2

ch_c．
∴可解得：h_a=

2

a

p(p-a)(p-b)(p-c)

，h_b=

2

b

p(p-a)(p-b)(p-c)

，h_c=

2

c

p(p-a)(p-b)(p-c)

．

点评：本题主要考查了余弦定理、三角形面积公式，平方差公式的应用，计算量较大，属于中档题．