
|
|
| 4 |
| 3 |
| 4 |
| 3 |


科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| m | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.查看答案和解析>>
科目:高中数学 来源: 题型:
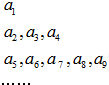 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
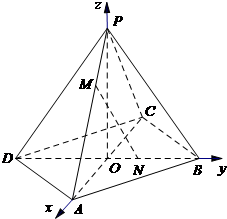 如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为3
如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为3| 2 |
| PM |
| PA |
| BN |
| BD |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| CB |
| e2 |
| e1 |
| CD |
| e1 |
| e2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com