
已知椭圆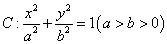 的离心率为
的离心率为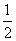 ,以原点为圆心,椭圆的短半轴长为
,以原点为圆心,椭圆的短半轴长为
半径的圆与直线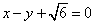 相切.
相切.
(1)求椭圆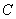 的方程;
的方程;
(2)设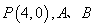 是椭圆
是椭圆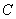 上关于
上关于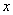 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接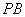 交椭圆
交椭圆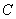 于另一点
于另一点 ,证明:直线
,证明:直线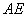 与
与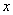 轴相交于定点
轴相交于定点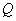 ;
;
(3)在(2)的条件下,过点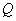 的直线与椭圆
的直线与椭圆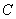 交于
交于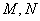 两点,求
两点,求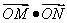 的取值范围.
的取值范围.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
假设在 秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于
秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于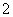 秒,手机就会受到干扰,则手机受到干扰的概率为( )
秒,手机就会受到干扰,则手机受到干扰的概率为( )
A.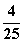 B.
B.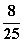 C.
C.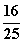 D.
D.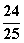
查看答案和解析>>
科目:高中数学 来源: 题型:
若点P在曲线y=x3-x上移动,则过P点的切线的倾斜角的取值范围是( )
(A)[0,π) (B)(0,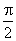 )∪[
)∪[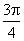 ,π)
,π)
(C)[0,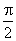 )∪(
)∪(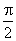 ,
, 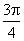 ] (D)[0,
] (D)[0,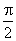 )∪[
)∪[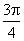 ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)的图象是连续不断的,且f(0)>0,f(1)·f(2)·f(4)<0,则下列说法中正确的是( )
A.函数f(x)在区间(0,1)内有零点
B.函数f(x)在区间(1,2)内有零点
C.函数f(x)在区间(0,2)内有零点
D.函数f(x)在区间(0,4)内有零点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com