
���� ����a��b��c�������ε����߳����ó�f��x��=cx[${��\frac{a}{c}��}^{x}$+${��\frac{b}{c}��}^{x}$-1]��cx��$\frac{a}{c}$+$\frac{b}{c}$-1����0���жϢ���ȷ��
����˵��a=2��b=3��c=4ʱ���������ε����߳�����a2=4��b2=9��c2=16���ܹ��������ε����߳����жϢ���ȷ��
��ABCΪֱ��������ʱc2=a2+b2��f��2n��=a2n+b2n-c2n=a2n+b2n-��a2+b2��n��0���жϢ۴���
��ABCΪ�۽�������ʱa2+b2-c2��0��f��1����0��f��2����0������f��x�������䣨1��2���ڴ�����㣬�жϢ���ȷ��
��� �⣺���ڢ٣���Ϊa��b��c�������ε������߳�������a+b��c��
����Ϊc��a��0��c��b��0������0��$\frac{a}{c}$��1��0��$\frac{b}{c}$��1��
���Ե�x�ʣ�-�ޣ�1��ʱ��f��x��=cx[${��\frac{a}{c}��}^{x}$+${��\frac{b}{c}��}^{x}$-1]��cx��$\frac{a}{c}$+$\frac{b}{c}$-1��
=cx•$\frac{a+b-c}{c}$��0���ʢ���ȷ��
���ڢڣ���a=2��b=3��c=4����a��b��c���Թ��������ε����߳���
��a2=4��b2=9��c2=16ȴ���ܹ��������ε����߳����ʢ���ȷ��
���ڢۣ�����ABCΪֱ�������Σ��������c2=a2+b2��
����n��N*��f��2n��=a2n+b2n-c2n=a2n+b2n-��a2+b2��n��0���ʢ۴���
���ڢܣ���Ϊc��a��0��c��b��0���ҡ�ABCΪ�۽������Σ�
����a2+b2-c2��0������f��1��=a+b-c��0��f��2��=a2+b2-c2��0��
�ʺ���f��x�������䣨1��2���ڴ�����㣬��?x0�ʣ�1��2����ʹf��x0��=0���ʢ���ȷ��
���ϣ���ȷ���۵����Ϊ�٢ڢܣ�
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼����������ٵ��ж����⣬Ҳ�����˺�����������Ӧ�����⣬���ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 39 | B�� | 21 | C�� | 39��21 | D�� | 21��36 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��ɫ | B�� | ��ɫ | C�� | ��ɫ�Ŀɱ��Դ� | D�� | ��ɫ�Ŀ����Դ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
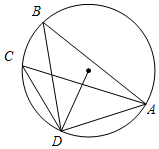 ��ͼ��Բ�ڽ��ı���ABCD�У�AD=DC=2BC=2��AB=3��
��ͼ��Բ�ڽ��ı���ABCD�У�AD=DC=2BC=2��AB=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=��\frac{1}{4}x$ | B�� | $y=��\frac{1}{3}x$ | C�� | $y=��\frac{1}{2}x$ | D�� | y=��x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=��\frac{{\sqrt{2}}}{2}x$ | B�� | $y=��\sqrt{2}x$ | C�� | y=��x | D�� | $y=��\frac{{\sqrt{5}}}{2}x$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ִ����ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ���ڣ�������
ִ����ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ���ڣ�������| A�� | 32��-1 | B�� | 32��$\frac{1}{2}$ | C�� | 8��1 | D�� | 8��-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com