练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)＝|log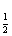x|的定义域是[a，b]，值域为[0,2]，对于区间[m，n]，称n－m为区间[m，n]的长度，则[a，b]长度的最小值为(　　)

    A.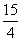                                                            B．3

    C．4                                                             D.


    D

    [解析]　令f(x)＝0得，x＝1，令f(x)＝2得，logx＝±2，∴x＝或4，∴当a＝，b＝1时满足值域为[0,2]，故选D.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

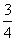
    科目：高中数学 来源： 题型：


    设角α，β是锐角，则“α＋β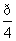＝”是“(1＋tanα)(1＋tanβ)＝2”的(　　)

    A．充分不必要条件                                      B．必要不充分条件

    C．充要条件                                                 D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝则f(f(3))＝(　　)

    A.                                                              B．3

    C.                                                             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝|x|x＋bx＋c，则下列命题中正确命题的序号有________．

    ①函数f(x)在R上有最小值；

    ②当b>0时，函数在R上是单调增函数；

    ③函数f(x)的图象关于点(0，c)对称；

    ④当b<0时，方程f(x)＝0有三个不同实数根的充要重要条件是b2>4|c|；

    ⑤方程f(x)＝0可能有四个不同实数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)满足条件：f(x)＋2f(－x)＝x，则f(x)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某化工厂生产某种产品，每件产品的生产成本是3元，根据市场调查，预计每件产品的出厂价为x元(7≤x≤10)时，一年的产量为(11－x)2万件，若该企业所生产的产品全部售出，则称该企业正常生产，但为了保护环境，用于治理污染的费用与产量成正比，比例系数为常数a(1≤a≤3)．

    (1)求该企业正常生产一年的利润L(x)与出厂价x的函数关系式；

    (2)当每件产品的出厂价定为多少元时，企业一年的利润最大，并求最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝log2(3x＋1)的值域为(　　)

    A．(0，＋∞)                                                B．[0，＋∞)

    C．(1，＋∞)                                                D．[1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在区间(0，＋∞)上的函数f(x)满足f()＝f(x1)－f(x2)，且当x>1时，f(x)>0.

    (1)求f(1)的值，并判断f(x)的单调性；

    (2)若f(4)＝2，求f(x)在[5,16]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝是奇函数．

    (1)求a，b的值；

    (2)求f(x)的单调区间，并加以证明；

    (3)求f(x)(x>0)的最值．

    查看答案和解析>>

    同步练习册答案