
分析 (1)由已知:点M到F(1,0)的距离与它到直线l':x=-1的距离相等,所以点M的轨迹C是以F为焦点,l'为准线的抛物线,由此能求出曲线C的方程;
(2)设直线AB方程为x=my+1.将直线AB的方程与抛物线的方程联立,得y2-4my-4=0.由此能够求出直线AB的斜率.
(3)由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于2S△AOB.由此能求出四边形OACB的面积最小值.
解答 解:(1)由已知条件知,点M到F(1,0)的距离与它到直线l':x=-1的距离相等,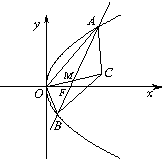
∴点M的轨迹C是以F为焦点,l'为准线的抛物线,
∴曲线C的方程为y2=4x(4分)
(2)依题意,设直线AB方程为x=my+1.
将直线AB的方程与抛物线的方程联立,消去x得y2-4my-4=0.
设A(x1,y1),B(x2,y2),所以 y1+y2=4m,y1y2=-4. ①
因为 $\overrightarrow{AF}=2\overrightarrow{FB}$,
所以 y1=-2y2. ②…(5分)
联立①和②,消去y1,y2,得m=±$\frac{\sqrt{2}}{4}$. …(8分)
所以直线AB的斜率是$k=±2\sqrt{2}$(4分)
(3)由点C与原点O关于点M对称,得M是线段OC的中点,
从而点O与点C到直线AB的距离相等,
所以四边形OACB的面积等于2S△AOB. …(9分)
因为2S△AOB=2×$\frac{1}{2}•|OF|×$|y1-y2|=4$\sqrt{1+{m}^{2}}$…(12分)
所以 m=0时,四边形OACB的面积最小,最小值是4. …(13分)
点评 本题考查抛物线的定义与方程,考查直线斜率的求法,考查四边形面积的最小值的求法,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-3,1] | C. | [-3,1] | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | y2-x2=1 | C. | y2-x2=1 | D. | ${y^2}-\frac{x^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设F1,F2为椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左、右焦点,动点P的坐标为(-1,m),过点F2的直线与椭圆交于A,B两点.
设F1,F2为椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左、右焦点,动点P的坐标为(-1,m),过点F2的直线与椭圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com