
分析 (1)利用二项展开式的通项公式Tr+1=${C}_{2n}^{r}$(-1)rx2n-2r,可求得(x-$\frac{1}{x}$)2n的展开式中常数项Tn+1=(-1)n•$\frac{(2n)!}{n!•n!}$,再利用排列数公式即可证得结论成立;
(2)利用二项展开式的通项公式,可求得(1+x)2n的展开式的中间一项.
解答 解:(1)∵(x-$\frac{1}{x}$)2n的展开式的通项为Tr+1=${C}_{2n}^{r}$(-1)rx2n-2r,
令2n-2r=0,得:n=r,
∴(x-$\frac{1}{x}$)2n的展开式中常数项是Tn+1=${C}_{2n}^{n}$(-1)n=(-1)n•$\frac{(2n)!}{n!•n!}$=(-2)n$\frac{1×3×5×…×(2n-1)}{n!}$.
(2))∵(1+x)2n的展开式共有2n+1项,展开式的中间一项是:
Tn+1=${C}_{2n}^{n}$•xn=$\frac{(2n)!}{n!•n!}$•xn=$\frac{{2}^{n}(2n-1)(2n-3)…3×1•n!}{n!•n!}$=$\frac{1×3×5×…×(2n-1)}{n!}$(2x)n.
点评 本题考查二项式定理的应用,着重考查二项展开式的通项公式及排列数公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
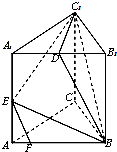 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com