
分析 求出命题p,q成立的等价条件,结合复合命题的真假关系进行求解即可.
解答 解:p:x2+4mx+1=0有两个不等的负根?$\left\{\begin{array}{l}{△=16{m}^{2}-4>0}\\{-4m<0}\end{array}\right.$,解得m>$\frac{1}{2}$----------(2分)
q:函数f(x)=-(m2-m+1)x在(-∞,+∞)上是增函数,则0<m2-m+1<1,解得0<m<1---(5分)
若p或q为真,p且q为假,则p,q为一真,一假,
(1)若p真,q假,则$\left\{\begin{array}{l}{m>\frac{1}{2}}\\{m≤0或m≥1}\end{array}\right.$,解得m≥1;----(8分)
(2)若p假,q真,则$\left\{\begin{array}{l}{m≤\frac{1}{2}}\\{0<m<1}\end{array}\right.$,解得0<m≤$\frac{1}{2}$----(11分)
综上,得m≥1,或0<m≤$\frac{1}{2}$---------------(12分)
点评 本题主要考查复合命题之间的关系的应用,求出命题p,q的等价条件是解决本题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
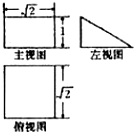
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 384种 | B. | 408种 | C. | 480种 | D. | 600种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是““?x∈R,x2-x-1≥0” | |
| C. | 当a<0时,幂函数y=xa在(0,+∞)上单调递减 | |
| D. | “φ=$\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)既偶函数,又是周期函数. | B. | f(x)的最大值为$\frac{\sqrt{3}}{2}$ | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)的图象关于直线x=π对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com