考点:数列与函数的综合,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:点列、递归数列与数学归纳法
分析:(1)求函数的导数,得到数列的递推关系式,根据数列{an}是等差数列的通项公式进行求解即可求a1的值:
(2)求出数列{an}的通项公式,利用不等式an+2n2≥0恒成立.利用参数分离法进行求解即可.
解答:
解:f′(x)=
-sinx-
+
,则f′(
)=4;
故a
n+1+a
n=πf′(
)+3=4n+3,
(1)若数列{a
n}是等差数列,
则a
n=a
1+(n-1)d,a
n+1=a
1+nd,
则a
n+1+a
n=a
1+(n-1)d+a
1+nd=2a
1+(2n-1)d=4n+3,
解得d=2,a
1=
.
(2)由a
n+1+a
n=4n+3,a
n+2+a
n+1=4n+7,
两式相减得a
n+2-a
n=4,
故数列{a
2n-1}是首项为a
1,公差为4的等差数列,
数列{a
2n}是首项为a
2,公差为4的等差数列,
又a
1+a
2=7,∴a
2=7-a
1,
∴a
n=
.
①当n为奇数时,a
n=2n-2+a
1,由a
n+2n
2≥0成立,
即2n-2+a
1+2n
2≥0,
转化为a
1≥-2n
2-2n+2,恒成立,
设f(n)=-2n
2-2n+2=-(n+
)
2+
,
∴f(n)
max=f(1)=-2,
∴a
1≥-2.
②当n为偶数时,a
n=2n+3-a
1,由a
n+2n
2≥0成立,
即2n+3-a
1+2n
2≥0,
转化为-a
1≥-2n
2-2n-3,恒成立,
设g(n)=-2n
2-2n-3=-(n+
)
2-
,
∴g(n)
max=g(2)=-15,
∴-a
1≥-15.
即a
1≤15,综上-2≤a
1≤15,
即a
1的取值范围是[-2,15].
点评:本题主要考查等差数列的通项公式的应用已经递推数列的应用,考查学生的运算和推理能力,求出数列的递推关系是解决本题的关键.



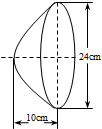 如图所示,汽车前灯反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处.已知灯口的直径是24cm,灯深10cm,那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )
如图所示,汽车前灯反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处.已知灯口的直径是24cm,灯深10cm,那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )