Question

17．如图，三棱锥PABC中，PC⊥平面ABC，PC=3，∠ACB=$\frac{π}{2}$，AC=2．D，E分别为线段AB，BC上的点，且CD=DE=$\sqrt{2}$，CE=2EB=2．
证明：（1）求三棱锥PABC的体积；
（2）证明DE⊥平面PCD．

Answer 1

分析 （1）作DF⊥BC，垂足为F，根据平行线的性质得出比例式计算AC，再代入体积公式计算三棱锥P-ABC的体积；
（2）根据勾股定理得出DE⊥CD，又PC⊥平面ABC得出PC⊥DE，故DE⊥平面PCD．

解答 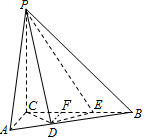解：（1）∵CD=DE=$\sqrt{2}$，CE=2EB=2，
∴CE²=CD²+DE²，
∴∠CDE=90°．
作DF⊥BC，垂足为F，则DF=$\frac{1}{2}$CE=1，
∵∠ACB=$\frac{π}{2}$，
∴DF∥AC，
∴$\frac{DF}{AC}$=$\frac{2}{3}$，
∴AC=$\frac{3}{2}$．
∴V_P-ABC=$\frac{1}{3}$S△_ABC•PC=$\frac{1}{3}$×$\frac{1}{2}$×3×$\frac{3}{2}$×3=$\frac{9}{4}$；
（2）证明：由PC⊥平面ABC，DE?平面ABC，
得PC⊥DE
由CE=2，CD=DE=$\sqrt{2}$，得△CDE为等腰直角三角形，
故CD⊥DE．
由PC∩CD=C，DE垂直于平面PCD内两条相交直线，
故DE⊥平面PCD．

点评 本题考查了线面垂直的判定，棱锥的体积计算，属于中档题．