
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 直接写出命题的逆否命题判断①;由复合命题的真假判断判断②;写出特称命题的否定判断③;由必要条件、充分条件及充要条件的判定方法判断④.
解答 解:①命题“若lgx=0,则x=l”的逆否命题为“若x≠1,则lgx≠0”,故命题①错误;
②若“p∧q”为假命题,则p,q中至少有一个为假命题,故命题②错误;
③命题p:?x∈R,使得sinx>l;则¬p:?x∈R,均有sinx≤1,故命题③正确;
④由x>2,得$\frac{1}{x}<\frac{1}{2}$,反之,若$\frac{1}{x}<\frac{1}{2}$,不一定有x>2,x也可能为负值,故“x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件,故④正确.
∴正确命题的个数是2.
故选:B.
点评 本题考查命题的真假判断与应用,考查了命题的否定与逆否命题,训练了必要条件、充分条件及充要条件的判定方法,是基础题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
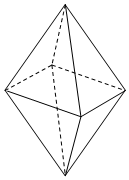 已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.
已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-tanx | B. | $y=cos(2x-\frac{π}{2})$ | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com