
分析 (1)过点F($\frac{1}{4}$,-$\frac{1}{8}$)任作直线y=k(x-$\frac{1}{4}$)-$\frac{1}{8}$,代入y=-2x2+x-$\frac{1}{8}$,整理,利用重心坐标公式,即可求△ABC的重心轨迹方程,并表示y=f(x)形式;
(2)证明0<xk<$\frac{3}{8}$(k=2,3,…),再利用放缩法即可证明结论.
解答 (1)解:设B(x1,y1),C(x2,y2),重心G(x,y),过点F($\frac{1}{4}$,-$\frac{1}{8}$)任作直线y=k(x-$\frac{1}{4}$)-$\frac{1}{8}$,
代入y=-2x2+x-$\frac{1}{8}$,整理可得2x2+(k-1)x-$\frac{k}{4}$=0,∴x1+x2=$\frac{1-k}{2}$,y1+y2=-$\frac{2{k}^{2}+1}{4}$,
∴3x=$\frac{1-k}{2}$+$\frac{1}{4}$,3y=-$\frac{2{k}^{2}+1}{4}$+$\frac{11}{8}$,
∴y=-6x2+3x;
(2)证明:∵0<x1<$\frac{1}{2}$,xk+1=f(xk)=-6xk2+3xk.
∴0<x2=-6x12+3x1=-6(x1-$\frac{1}{4}$)2+$\frac{3}{8}$;
假设0<xk<$\frac{3}{8}$成立,则0<xk+1=-3xk(1-2xk)≤$\frac{3}{2}•[\frac{2{x}_{k}+(1-2{x}_{k})}{2}]^{2}$=$\frac{3}{8}$,
当且仅当xk=$\frac{1}{4}$等号成立,
∴0<xk<$\frac{3}{8}$(k=2,3,…),
∴$\sum_{k=1}^{n}$xk+1k≤$\sum_{k=1}^{n}$($\frac{3}{8}$)k=$\frac{3}{5}$[1-($\frac{3}{8}$)n]<$\frac{3}{5}$.
点评 本题考查轨迹方程,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
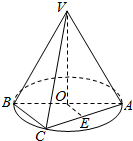 如图AB是圆O的直径,点C是圆O上不同于A,B的一点,点V是圆O所在平面外一点.
如图AB是圆O的直径,点C是圆O上不同于A,B的一点,点V是圆O所在平面外一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | (0,-$\frac{1}{4}$) | C. | (0,-$\frac{1}{2}$) | D. | (0,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
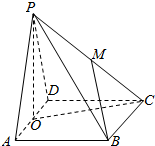 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{a}{2}$,0) | B. | ($\frac{a}{4}$,0) | C. | (0,$\frac{a}{2}$) | D. | (0,$\frac{a}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com