
 已知S为执行如图所示的程序框图输出的结果,则二项式(S$\sqrt{x}$-$\frac{3}{\sqrt{x}}$)6的展开式中常数项的系数是( )
已知S为执行如图所示的程序框图输出的结果,则二项式(S$\sqrt{x}$-$\frac{3}{\sqrt{x}}$)6的展开式中常数项的系数是( )| A. | -20 | B. | 20 | C. | -$\frac{20}{3}$ | D. | 60 |
分析 模拟程序框图的运行过程,求出输出a的值,再求二项式的展开式中常数项的值.
解答 解:模拟程序框图的运行过程,如下:
i=0,s=1,i=1,i<4,是,s=$\frac{1-2}{1}$=-1;
i=2,2<4,是,s=$\frac{-1-2}{-1}$=3;
i=3,3<4,是,s=$\frac{3-2}{3}$=$\frac{1}{3}$;
i=4,4<4,否,退出循环,输出s的值为$\frac{1}{3}$.
∴二项式($\frac{1}{3}$$\sqrt{x}$-$\frac{3}{\sqrt{x}}$)6的展开式中的通项是
Tr+1=${C}_{6}^{r}$•($\frac{\sqrt{3}}{3}$)6-r•(-$\frac{3}{\sqrt{x}}$)r=(-1)r•${C}_{6}^{r}$•($\frac{1}{3}$)6-2r•x3-r;
令3-r=0,得r=3;
∴常数项是T4=(-1)3•${C}_{6}^{3}$•($\frac{1}{3}$)0=-20.
故选:A.
点评 本题考查了出现框图的应用以及二项式定理的应用问题,解题时应模拟程序框图的运行过程,并利用二项式的通项公式进行计算,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
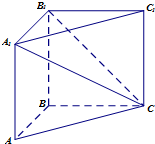 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 与m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com