
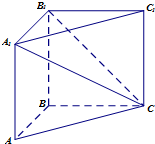
 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.  名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 平均气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 25 | 35 | 37 | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 用细钢管焊接而成的花坛围栏构件如右图所示,它的外框是一个等腰梯形PQRS,内部是一段抛物线和一根横梁.抛物线的顶点与梯形上底中点是焊接点O,梯形的腰紧靠在抛物线上,两条腰的中点是梯形的腰、抛物线以及横梁的焊接点A,B,抛物线与梯形下底的两个焊接点为C,D.已知梯形的高是40厘米,C、D两点间的距离为40厘米.
用细钢管焊接而成的花坛围栏构件如右图所示,它的外框是一个等腰梯形PQRS,内部是一段抛物线和一根横梁.抛物线的顶点与梯形上底中点是焊接点O,梯形的腰紧靠在抛物线上,两条腰的中点是梯形的腰、抛物线以及横梁的焊接点A,B,抛物线与梯形下底的两个焊接点为C,D.已知梯形的高是40厘米,C、D两点间的距离为40厘米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知S为执行如图所示的程序框图输出的结果,则二项式(S$\sqrt{x}$-$\frac{3}{\sqrt{x}}$)6的展开式中常数项的系数是( )
已知S为执行如图所示的程序框图输出的结果,则二项式(S$\sqrt{x}$-$\frac{3}{\sqrt{x}}$)6的展开式中常数项的系数是( )| A. | -20 | B. | 20 | C. | -$\frac{20}{3}$ | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于点($\frac{5π}{12}$,0)对称 | ||
| C. | 关于直线x=$\frac{5π}{12}$对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com