
分析 (1)根据题目条件列式求得椭圆方程和双曲线方程.
(2)A (-5,0)B (5,0)设M(x,y)为椭圆上点,P(2x-5,2y)代入椭圆方程,求得坐标,再利用三角形面积公式求得三角形面积.
解答 解:(1)设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$双曲线方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,
$\left\{{\begin{array}{l}{{a^2}+{b^2}=34}\\{\frac{c}{a}=\frac{4}{5}}\end{array}}\right.$,
即$\left\{{\begin{array}{l}{{a^2}+{b^2}=34}\\{\frac{{{a^2}-{b^2}}}{a^2}=\frac{16}{25}}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{{a^2}=25}\\{{b^2}=9}\end{array}}\right.$,
所以椭圆方程 $\frac{x^2}{25}+\frac{y^2}{9}=1$双曲线方程$\frac{x^2}{25}-\frac{y^2}{9}=1$;
(2)A (-5,0)B (5,0)设M(x,y)为椭圆上点,P(2x-5,2y),
代入$\left\{{\begin{array}{l}{\frac{{(2x-5{)^2}}}{25}-\frac{{4{y^2}}}{9}=1}\\{\frac{x^2}{25}+\frac{y^2}{9}=1}\end{array}}\right.$得:2x2-5x-26=0,解得x1=5(舍去),或 $\left\{{\begin{array}{l}{{x_2}=-\frac{5}{2}}\\{{y_2}=\frac{{3\sqrt{3}}}{2}}\end{array}}\right.$,
${S_{△ABM}}=\frac{1}{2}×10×\frac{{3\sqrt{3}}}{2}=\frac{{15\sqrt{3}}}{2}$.
点评 本题主要考查圆锥曲线的性质应用和圆锥曲线中三角形面积的求法,属于中档题型.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{5}{3}$ | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
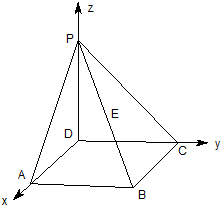 PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )| A. | (1,1,2) | B. | (2,2,1) | C. | (1,1,1) | D. | $(1\;,\;1\;,\;\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
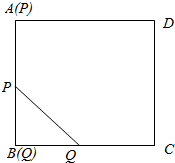 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com