
分析 由约束条件画出可行域,然后利用(x-3)2+(y-3)2的几何意义,即可行域内的动点与定点(3,3)距离的平方求解.
解答 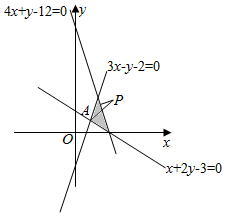 解:由约束条件$\left\{{\begin{array}{l}{3x-y-2≥0}\\{x+2y-3≥0}\\{4x+y-12≤0}\end{array}}\right.$作出可行域如图,
解:由约束条件$\left\{{\begin{array}{l}{3x-y-2≥0}\\{x+2y-3≥0}\\{4x+y-12≤0}\end{array}}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{3x-y-2=0}\\{x+2y-3=0}\end{array}\right.$,解得A(1,1).
(x-3)2+(y-3)2的几何意义为可行域内的动点与定点(3,3)距离的平方.
∵|PA|=$\sqrt{(3-1)^{2}+(3-1)^{2}}=\sqrt{8}$,
而P到x轴上的点(3,0)的距离为3,
点P(3,3)到直线4x+y-12=0的距离为$\frac{|4×3+3-12|}{\sqrt{17}}=\frac{3}{\sqrt{17}}$.
∴(x-3)2+(y-3)2的范围是[$\frac{9}{17},9$].
故答案为:[$\frac{9}{17},9$].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | A∩B={-1} | B. | (∁RA)∪B=(-∞,0) | C. | A∪B=(0,+∞) | D. | (∁RA)∩B={-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (4,+∞) | C. | (-∞,4] | D. | (-∞,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(3x-$\frac{3π}{4}$) | B. | y=sin(3x+$\frac{π}{4}$) | C. | y=sin(3x-$\frac{π}{4}$) | D. | y=sin(3x+$\frac{3π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com