
| A. | 35 | B. | 33 | C. | 31 | D. | 29 |
分析 运用等差中项和等比中项的性质,以及等比数列的通项公式,{an}为正项等比数列,设公比为q,得到首项和公比的方程,解方程可得首项和q,再由等比数列的求和公式计算即可得到所求值.
解答 解:a3与a5的等比中项是2,且a4与2a7的等差中项为$\frac{5}{4}$,
则a3a5=4,a4+2a7=$\frac{5}{2}$,
{an}为正项等比数列,设公比为q,
可得a1q2•a1q4=4,a1q3+2a1q6=$\frac{5}{2}$,
解得q=$\frac{1}{2}$,a1=16,
则S5=$\frac{16(1-\frac{1}{{2}^{5}})}{1-\frac{1}{2}}$=31.
故选:C.
点评 本题考查等差中项和等比中项的性质,以及等比数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
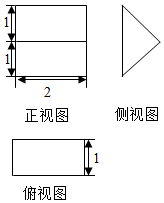 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={(3,2)},N={(2,3)} | B. | M={2,3},N={3,2} | ||
| C. | M={(x,y)|x+y=1},N={y|x+y=1} | D. | M={2,3},N={(2,3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0<a | B. | x0>b | C. | x0<c | D. | x0>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-a2b)2•(-ab2)3=-a7b8 | B. | [-(a3)2•(-b2)3]3=a18b18 | ||
| C. | (-a3)2•(-b2)3=a6b6 | D. | (-a2b3)3÷(-ab2)3=a3b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
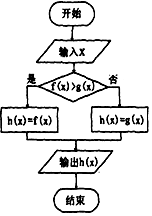
| A. | -$\frac{{\sqrt{3}}}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com