
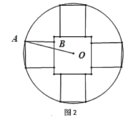
【题目】从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设![]() ,五个正方形的面积和为S.
,五个正方形的面积和为S.

(1)求面积S关于![]() 的函数表达式,并求定义域;
的函数表达式,并求定义域;
(2)求面积S的最小值及此时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() 的取值范围为
的取值范围为![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 时,面积S有最小值为
时,面积S有最小值为![]() .
.
【解析】
(1)构造直角三角形,利用小圆直径与三角函数分别求出大、小正方形的边长,即可求得五个正方形的面积表达式,由小正方形边长小于内嵌一个大正方形的边长可求得![]() 的取值范围;(2)利用降幂公式及辅助角公式化简面积表达式为正弦型函数,当
的取值范围;(2)利用降幂公式及辅助角公式化简面积表达式为正弦型函数,当![]() 时S取最小值,此时求出
时S取最小值,此时求出![]() 的值然后求出
的值然后求出![]() ,由二倍角的正弦公式可求得
,由二倍角的正弦公式可求得![]() .
.
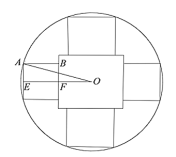
(1)过点O分别作小正方形边,大正方形边的垂线,垂足分别为E,F,
因为内嵌一个大正方形孔的中心与同心圆圆心重合,
所以点E,F分别为小正方形和大正方形边的中点,
所以小正方形的边长为![]() ,
,
大正方形的边长为![]() ,
,
所以五个正方形的面积和为![]() ,
,
![]() ,
,
因为小正方形边长小于内嵌一个大正方形的边长,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() ,
,![]() ,
,
所以面积S关于![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() 的取值范围为
的取值范围为![]() ,
,![]() ,
,![]() .
.
(2)法一:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,此时
,此时![]() ,因为
,因为![]() ,所以
,所以
![]() ,所以
,所以![]() ,
,
所以![]() ,
,
则![]() ,化简得:
,化简得:![]() ,
,
由此解得:![]() ,
,
因为![]() ,所以
,所以![]() ,
,
答:面积S最小值为![]() ,
,
法二:![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,
,
令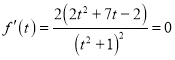 ,得:
,得:![]() ,
,
t |
|
|
|
| - | 0 | + |
|
| 极小值 |
|
所以![]() 时,面积S最小值为
时,面积S最小值为![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 是平面
是平面![]() 和平面
和平面![]() 的交线,异面直线
的交线,异面直线![]() ,
,![]() 分别在平面
分别在平面![]() 和平面
和平面![]() 内.
内.
命题![]() :直线
:直线![]() ,
,![]() 中至多有一条与直线
中至多有一条与直线![]() 相交;
相交;
命题![]() :直线
:直线![]() ,
,![]() 中至少有一条与直线
中至少有一条与直线![]() 相交;
相交;
命题![]() :直线
:直线![]() ,
,![]() 都不与直线
都不与直线![]() 相交.
相交.
则下列命题中是真命题的为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 是线段
是线段![]() 的中点.
的中点.
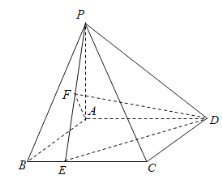
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
①求线段![]() 的长;
的长;
②求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其右顶点为
,其右顶点为![]() ,下顶点为
,下顶点为![]() ,定点
,定点![]() ,
,![]() 的面积为
的面积为![]() ,过点
,过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.
两点.
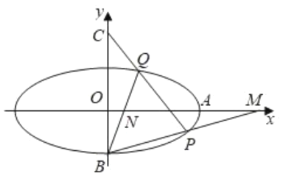
(1)求椭圆![]() 的方程;
的方程;
(2)试探究![]() 的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
的横坐标的乘积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“三分损益法”是古代中国发明制定音律时所用的方法,其基本原理是:以一根确定长度的琴弦为基准,取此琴强长度的![]() 得到第二根琴弦,第二根琴弦长度的
得到第二根琴弦,第二根琴弦长度的![]() 为第三根琴弦,第三根琴弦长度的
为第三根琴弦,第三根琴弦长度的![]() 为第四根琴弦.第四根琴弦长度的
为第四根琴弦.第四根琴弦长度的![]() 为第五根琴弦.琴弦越短,发出的声音音调越高,这五根琴弦发出的声音按音调由低到高分别称为“官、商、角(jué)、微(zhǐ)、羽”,则“角"和“徵”对应的琴弦长度之比为( )
为第五根琴弦.琴弦越短,发出的声音音调越高,这五根琴弦发出的声音按音调由低到高分别称为“官、商、角(jué)、微(zhǐ)、羽”,则“角"和“徵”对应的琴弦长度之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 为矩形,四边形
为矩形,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
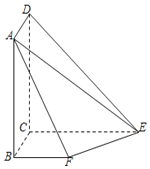
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() ,平面
,平面![]() 平面
平面![]() .
.
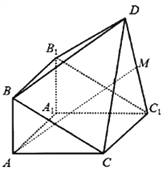
(Ⅰ)求证: ![]() ;
;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的
个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,关于
的图象,关于![]() 的说法有:①函数
的说法有:①函数![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象的一条对称轴是
的图象的一条对称轴是![]() ;③函数
;③函数![]() 在
在![]() 上的最上的最小值为
上的最上的最小值为![]() ;④函数
;④函数![]() 上单调递增,则以上说法正确的个数是( )
上单调递增,则以上说法正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com