
| x | 2 | 3 | 4 | 5 | 6 |
| y | 22 | 38 | 55 | 65 | 70 |
分析 (1)根据所给的数据,做出变量x,y的平均数,根据最小二乘法做出线性回归方程的系数b,在根据样本中心点一定在线性回归直线上,求出a的值,求得线性回归方程;
(2)当自变量为10时,代入线性回归方程,求出维修费用.
解答 解:(1)列表如下:
| i | 1 | 2 | 3 | 4 | 5 |
| xi | 2 | 3 | 4 | 5 | 6 |
| yi | 22 | 38 | 55 | 65 | 70 |
| xiyi | 44 | 114 | 220 | 325 | 420 |
| $x_i^2$ | 4 | 9 | 16 | 25 | 36 |
| $\overline x=4$,$\overline y=50$,$\sum_{i=1}^5{x_i^2}=90$,$\sum_{i=1}^5{{x_i}{y_i}}=1123$ | |||||
点评 本题考查最小二乘法求回归方程,考查回归方程的应用,解题时要认真审题,注意散点图的灵活运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{3}$ | B. | $5\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
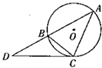 如图,点ABC都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为( )
如图,点ABC都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|α=2kπ-$\frac{π}{4}$,k∈Z} | B. | {α|α=2kπ+$\frac{π}{4}$,k∈Z} | C. | {α|α=2kπ-$\frac{5π}{4}$,k∈Z} | D. | {α|α=2kπ+$\frac{5π}{4}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
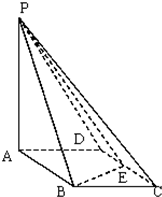 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com