Question

13．已知，在直角梯形ABCD中，BC∥AD，BC⊥CD，∠BAD=$\frac{π}{3}$，AB=2BC=2，动点P在以C为圆心且与直线BD相切的圆上运动，若$\overrightarrow{AP}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$，则α+β的取值范围是（　　）

• A． [0，1]
• B． [0，2]
• C． [1，2]
• D． （-∞，1]∪[2，+∞）

Answer 1

分析 建立直角坐标系，写出点的坐标，求出BD的方程，求出圆的方程；设出P的坐标，求出三个向量的坐标，将P的坐标用α，β表示，代入圆内方程求出范围．

解答 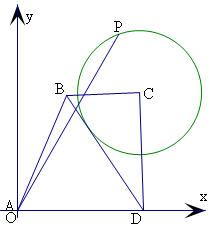解：以A为坐标原点，DA为x轴建立平面直角坐标系，
在直角梯形ABCD中，BC∥AD，BC⊥CD，∠BAD=$\frac{π}{3}$，
AB=2BC=2，
A（0，0），D（2，0），C（2，$\sqrt{3}$），B（2cos$\frac{π}{3}$，2sin$\frac{π}{3}$）
即有B（1，$\sqrt{3}$），
直线BD的方程为$\sqrt{3}$x+y-2$\sqrt{3}$=0，
C到BD的距离d=$\frac{|2\sqrt{3}+\sqrt{3}-2\sqrt{3}|}{\sqrt{3+1}}$=$\frac{\sqrt{3}}{2}$，
∴以点C为圆心，且与直线BD相切的圆方程为：（x-2）²+（y-$\sqrt{3}$）²=$\frac{3}{4}$，
设P（x，y），则$\overrightarrow{AP}$=（x，y），$\overrightarrow{AD}$=（2，0），
$\overrightarrow{AB}$=（1，$\sqrt{3}$），
若$\overrightarrow{AP}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$，
∴（x，y）=（α+2β，$\sqrt{3}$α）
∴x=α+2β，y=$\sqrt{3}$α，
∵P在圆内或圆上，
∴（α+2β-2）²+（$\sqrt{3}$α-$\sqrt{3}$）²≤$\frac{3}{4}$，
设α+β=t，得β=t-α，
代入上式化简整理得4α²-（4t+2）α+4t²-8t+$\frac{25}{4}$≤0，
若要上述不等式有实数解，
则△=（4t+2）²-4×4×（4t²-8t+$\frac{25}{4}$）≥0，
化简得t²-3t+2≤0，
解得1≤t≤2，
即1≤α+β≤2，
∴α+β取值范围是[1，2]．
故选：C．

点评 通过建立直角坐标系将问题代数化、考查直线与圆相切的条件、考查向量的坐标公式．