
设数列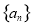 的前
的前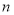 项和为
项和为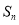 ,对任意的正整数
,对任意的正整数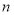 ,都有
,都有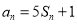 成立,记
成立,记 。
。
(1)求数列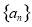 与数列
与数列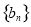 的通项公式;
的通项公式;
(2)记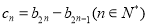 ,设数列
,设数列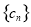 的前
的前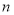 项和为
项和为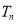 ,求证:对任意正整数
,求证:对任意正整数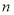 都有
都有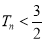 ;
;
(1) ,
, ;(2)祥见解析.
;(2)祥见解析.
【解析】
试题分析:(1)由已知及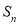 与
与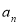 的关系:
的关系: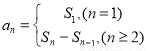 ,令n=1可求得
,令n=1可求得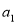 的值,再将已知等式中的n换成n+1得
的值,再将已知等式中的n换成n+1得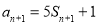 ,然后与已知式子:
,然后与已知式子: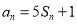 相减得到:
相减得到: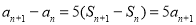 ,从而可得到:
,从而可得到: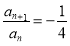 ,这说明数列
,这说明数列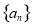 是公比为
是公比为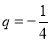 的等比数列,所以就可写出数列
的等比数列,所以就可写出数列 的通项公式,再代入
的通项公式,再代入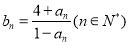 就可得到数列
就可得到数列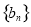 的通项公式;(2)由(1)的结果,结合
的通项公式;(2)由(1)的结果,结合 就可得到数列
就可得到数列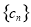 的通项公式,如果其前n项和可求,则先求出其前n项和
的通项公式,如果其前n项和可求,则先求出其前n项和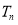 再与
再与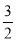 比较大小;若直接求和比较难办,则注意思考先用放缩法将数列
比较大小;若直接求和比较难办,则注意思考先用放缩法将数列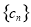 的通项公式放大成一个可求和的数列,则
的通项公式放大成一个可求和的数列,则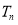 小于此数列的前n项和,而此此数列的前n项和恰好是小于或等于
小于此数列的前n项和,而此此数列的前n项和恰好是小于或等于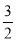 的,因此在放大的时候一定要注意适当放大且能求和是关键.
的,因此在放大的时候一定要注意适当放大且能求和是关键.
试题解析:(1)当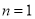 时,
时, 1分
1分
又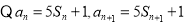
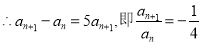 3分
3分
∴数列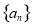 是首项为
是首项为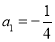 ,公比为
,公比为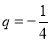 的等比数列, 4分
的等比数列, 4分
∴ ,
, 6分
6分
(2)由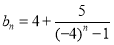 得 7分
得 7分
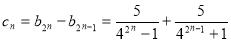
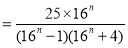
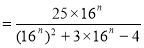
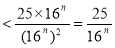 10分
10分
又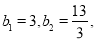 当
当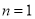 时,
时,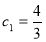 ,
,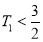 , 11分
, 11分
当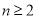 时,
时,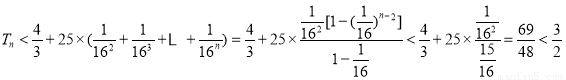
∴对任意正整数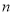 都有
都有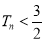 。 14分
。 14分
考点:1.等比数列;2.数列求和;3.不等式的证明.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源:2016届广东省高一下学期期中考试文科数学试卷(解析版) 题型:选择题
长方体的表面积是24,所有棱长的和是24,则对角线的长是( ).
A.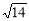 B.4 C.3
B.4 C.3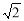 D.2
D.2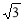
查看答案和解析>>
科目:高中数学 来源:2016届广东省梅州市高一上学期质检数学试卷(解析版) 题型:填空题
某中学为了解学生数学课程的学习情况,在3 000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测这3 000名学生在该次数学考试中成绩小于60分的学生数是_________
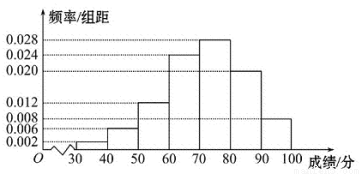
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期第一次阶段考试数学试卷(解析版) 题型:选择题
若圆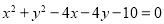 上至少有三个不同点到直线
上至少有三个不同点到直线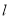 :
: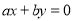 的距离为
的距离为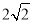 ,则直线
,则直线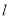 的斜率的取值范围是 ( )
的斜率的取值范围是 ( )
A.[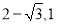 ] B.
] B.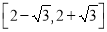 C.[
C.[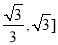 D.
D.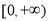
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com