
分析 当x0>0时,f(x0)=lgx0=1,;当x0<0时,$f({x}_{0})={{x}_{0}}^{-2}=1$.由此能求出x0的值.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{lgx,x>0}\\{{x}^{-2},x<0}\end{array}\right.$,f(x0)=1,
∴当x0>0时,f(x0)=lgx0=1,解得x0=10;
当x0<0时,$f({x}_{0})={{x}_{0}}^{-2}=1$,解得x0=1,不成立.
综上,x0=10.
∴x0的值是10.
故答案为:10.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
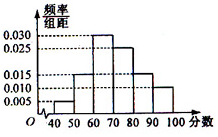 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A. | 588 | B. | 480 | C. | 450 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [0,1] | C. | [$\frac{2}{3}$,+∞) | D. | [1,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
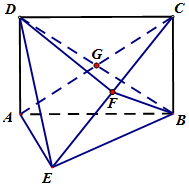 如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com