
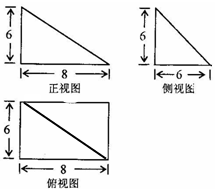
 已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示). 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 减少3.5个单位 | B. | 增加2个单位 | C. | 增加3.5个单位 | D. | 减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | $[3+2\sqrt{2}\;\;,\;\;+∞)$ | C. | [6,+∞) | D. | $(4\;\;,\;\;3+2\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
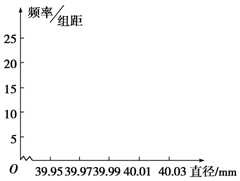 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | ||
| [39.97,39.99) | 4 | ||
| [39.99,40.01) | 10 | ||
| [40.01,40.03] | 4 | ||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com