
分析 可得直线分别过定点(0,0)和(1,3)且垂直,可得|PA|2+|PB|2=10.三角换元后,由三角函数的知识可得$\sqrt{3}$PA+PB的最大值.
解答 解:由题意可得A(0,0),由于直线mx-y-m+3=0,即 m(x-1)-y+3=0,显然经过定点B(1,3),
注意到动直线x+my=0和动直线mx-y-m+3=0始终垂直,P又是两条直线的交点,
则有PA⊥PB,∴|PA|2+|PB|2=|AB|2=10.
设∠ABP=θ,则|PA|=$\sqrt{10}$sinθ,|PB|=$\sqrt{10}$cosθ.
∵|PA|≥0且|PB|≥0,可得θ∈[0,$\frac{π}{2}$],
∴$\sqrt{3}$|PA|+|PB|=$\sqrt{30}$sinθ+$\sqrt{10}$cosθ=2$\sqrt{10}$[$\frac{\sqrt{3}}{2}$sinθ+$\frac{1}{2}$cosθ)=2$\sqrt{10}$sin(θ+$\frac{π}{6}$),
∵θ∈[0,$\frac{π}{2}$],∴θ+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],∴当θ+$\frac{π}{6}$=$\frac{π}{2}$时,2$\sqrt{10}$sin(θ+$\frac{π}{6}$)取得最大值为 2$\sqrt{10}$,
故答案为:2$\sqrt{10}$.
点评 本题考查直线过定点问题,涉及直线的垂直关系和三角恒等变换,正弦函数的定义域和值域,属中档题.


科目:高中数学 来源: 题型:解答题
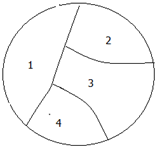 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=(0,+∞) | B. | (∁RA)∪B=(-∞,0] | C. | (∁RA)∩B={-1,0} | D. | (∁RA)∩B={1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,$\frac{1}{3}$] | C. | (-∞,$\frac{1}{3}$]∪[1,+∞) | D. | [$\frac{1}{3}$,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com