
| A. | 3 | B. | 1 | C. | 1或3 | D. | -1 |
分析 由f′(x)=3x2-4cx+c2,根据函数f(x)=x(x-c)2在x=1处有极小值,得f′(1)=3-4c+c2=0,求出c=1或c=3,再把c=1和c=3分别代入f′(x)中,由此利用导数性质能求出结果.
解答 解:∵函数f(x)=x(x-c)2=x3-2cx2+c2x,
∴f′(x)=3x2-4cx+c2,
∵函数f(x)=x(x-c)2在x=1处有极小值,
∴f′(1)=3-4c+c2=0,
解得c=1或c=3,
当c=1时,f′(x)=3x2-4x+1,
由f′(x)>0,得x<$\frac{1}{3}$或x>1;由f′(x)<0,得$\frac{1}{3}<x<1$.
∴增区间是(-∞,$\frac{1}{3}$),(1,+∞),减区间是($\frac{1}{3}$,1),
当x=1时,f(x)取极小值,故c=1成立;
当c=3时,f′(x)=3x2-12x+9,
由f′(x)>0,得x<1或x>3;由f′(x)<0,得1<x<3.
∴增区间是(-∞,1),(3,+∞),减区间是(1,3),
当x=1时,f(x)取极大值,故c=3不成立.
综上:实数c为1.
故选:B.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

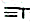 ”表示36,“
”表示36,“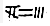 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )| A. |  | B. | 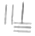 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x与y正相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y负相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {-1,1,2} | C. | {-1,0,2} | D. | {-1,0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com