练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知平面直角坐标系中，曲线的方程为，以原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为．若将曲线上的所有点的横坐标缩小到原来的一半，纵坐标伸长到原来的倍，得曲线．

    （1）写出直线和曲线的直角坐标方程；

    （2）设点， 直线与曲线的两个交点分别为，，求的值．

    【答案】（1），（2）

    【解析】

    （1）转化直线的极坐标方程为，利用极坐标方程与直角坐标方程转化公式得直线的直角坐标方程；设点在曲线上，点为坐标变换后点的对应点，由题意得，代入化简即可得解；

    （2）写出直线的参数方程,(t为参数)，代入的直角坐标方程，由根与系数的关系可得，，转化条件即可得解.

    （1）直线的极坐标方程可化为，

    直线的直角坐标方程为；

    设点在曲线上，点为坐标变换后点的对应点，

    则，，化简得，

    曲线的直角坐标方程为；

    （2）由题意点在直线上，

    则直线的参数方程为,(t为参数)，

    将直线的参数方程代入曲线的直角坐标方程可得：，，

    则，，

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目，按照国际田径联合会制定的田径运动全能评分表计分，然后将各个单项的得分相加，总分多者为优胜．下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图．

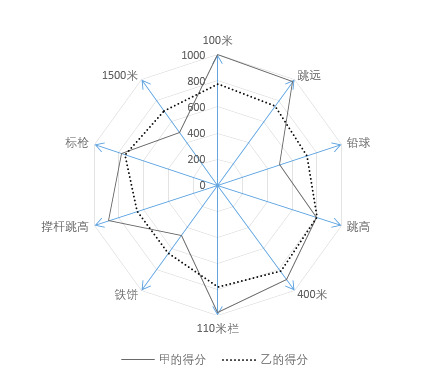
    下列说法错误的是（ ）

    A.在100米项目中，甲的得分比乙高

    B.在跳高和标枪项目中，甲、乙的得分基本相同

    C.甲的各项得分比乙更均衡

    D.甲的总分高于乙的总分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行四边形中，，，为边的中点，将沿直线翻折成，设为线段的中点．则在翻折过程中，给出如下结论：

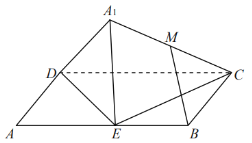
    ①当不在平面内时，平面；

    ②存在某个位置，使得；

    ③线段的长是定值；

    ④当三棱锥体积最大时，其外接球的表面积为．

    其中，所有正确结论的序号是______．（请将所有正确结论的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某省即将实行新高考，不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响，对该校2018级的1000名学生进行调查，收集到相关数据如下：

    （1）根据以上提供的信息，完成列联表，并完善等高条形图；

    选物理

    不选物理

    总计

    数学成绩优秀

    数学成绩不优秀

    260

    总计

    600

    1000

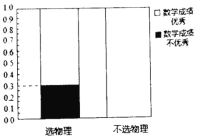
    （2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？

    附：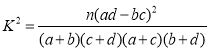

    临界值表：

    0.10

    0.05

    0.010

    0.005

    0.001

    2.706

    3.841

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为坐标原点，动点在圆上，过作轴的垂线，垂足为，点满足．

    （1）求点的轨迹的方程；

    （2）直线上的点满足．过点作直线垂直于线段交于点．

    （ⅰ）证明：恒过定点；

    （ⅱ）设线段交于点，求四边形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用组成没有重复数字的五位数abcde，其中随机取一个五位数，满足条件的概率为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为助力湖北新冠疫情后的经济复苏，某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价，用不同的单价在平台试销，得到如下数据：

    单价（元/件）

    8

    8.2

    8.4

    8.6

    8.8

    9

    销量（万件）

    90

    84

    83

    80

    75

    68

    （1）根据以上数据，求关于的线性回归方程；

    （2）若该产品成本是4元/件，假设该产品全部卖出，预测把单价定为多少时，工厂获得最大利润?

    （参考公式：回归方程，其中）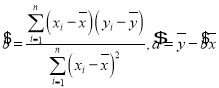

    查看答案和解析>>

    科目：高中数学 来源： 题型：

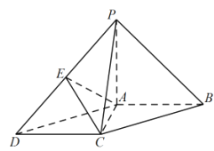
    【题目】如图，在四棱锥中，底面，底面为平行四边形，，且，，是棱的中点.

    （1）求证：平面；

    （2）求直线与平面所成角的正弦值；

    （3）在线段上(不含端点)是否存在一点，使得二面角的余弦值为？若存在，确定的位置；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为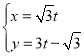（为参数），以坐标原点为极点，轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线的极坐标方程为.

    (1)求直线的极坐标方程和曲线的参数方程；

    (2)若，直线与曲线交于两点，求的值.

    查看答案和解析>>

    同步练习册答案