
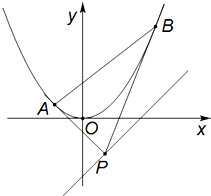
 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,分析 (Ⅰ)设A(x1,${x}_{1}^{2}$),B(x2,${x}_{2}^{2}$),P(x0,y0),可求切线PA,切线PB的方程,可得2x0=x1+x2,y0=x1x2,设直线AB的方程是y=kx+b,代入x2=y得x0=$\frac{k}{2}$,y0=-b,代入y0=x0-1得-b=$\frac{k}{2}$-1,从而可求直线AB的方程,即可得解.
(Ⅱ)由两点间距离公式可求|AB|,由点到直线的距离公式可求点P到直线AB的距离d,由三角形面积公式及基本不等式即可得解.
解答 (Ⅰ)证明:设A(x1,${x}_{1}^{2}$),B(x2,${x}_{2}^{2}$),P(x0,y0),
因为y′=(x2)′=2x,所以切线PA的方程是y-x12=2x1(x-x1),
即y+x12=2x1x ①,同理切线PB的方程是y+x22=2x2x ②--------(3分)
由①②得2x0=x1+x2,y0=x1x2,显然直线AB存在斜率.
设直线AB的方程是y=kx+b,代入x2=y得x2-kx-b=0,
所以x1+x2=k,x1x2=-b,即x0=$\frac{k}{2}$,y0=-b,③
代入y0=x0-1得-b=$\frac{k}{2}$-1-------------------------------------------(5分)
即直线AB的方程是y-1=k(x-$\frac{1}{2}$),恒过定点($\frac{1}{2}$,1)-------------(6分)
(Ⅱ)解:|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+{(x}_{1}^{2}{-x}_{2}^{2})^{2}}$
=$\sqrt{({x}_{1}-{x}_{2})^{2}[1+({x}_{1}+{x}_{2})^{2}]}$
=$\sqrt{[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}][1+({x}_{1}+{x}_{2})^{2}]}$
=$\sqrt{({k}^{2}+4b)(1+{k}^{2})}$
=$\sqrt{({k}^{2}-2k+4)(1+{k}^{2})}$--------------------(9分)
点P到直线AB的距离是d=$\frac{|k({x}_{0}-\frac{1}{2})-{y}_{0}+1|}{\sqrt{1+{k}^{2}}}$=$\frac{|{k}^{2}-2k+4|}{2\sqrt{1+{k}^{2}}}$-----(10分)
△PAB的面积=$\frac{1}{2}$|AB|•d=$\frac{1}{4}•|{k}^{2}-2k+4{|}^{\frac{3}{2}}$=$\frac{1}{4}|(k-1)^{2+3}{|}^{\frac{3}{2}}$$≥\frac{3\sqrt{3}}{4}$,
当k=1时△PAB的面积取得最小值$\frac{3\sqrt{3}}{4}$.-----------------------(12分)
点评 本题主要考查了直线与圆锥曲线的关系,两点间距离公式,点到直线距离公式,直线的方程等知识的应用,属于基本知识的考查.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{7π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,$\frac{4}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com