
分析 (Ⅰ)先由f′(x)>0,再根据函数f(x)在[-2,2]上为单调函数,将原问题转化为a≤2x2+4x-1=2(x+1)2-3在[-2,2]上恒成立问题,解之即得;
(Ⅱ)f(x)有两个不同的极值点m,n,即f′(x)=0有两个不等的实根,根据判别式和根与系数的关系,即可求出a的取值范围,在利用导数求出f(a)的取值范围即可.
解答 解:(Ⅰ)函数f(x)在[-2,2]上是单调增函数,
∴f′(x)=(2x2+4x-a-1)ex≥0在[-2,2]上恒成立,
即2x2+4x-a-1≥0,
∴a≤2x2+4x-1=2(x+1)2-3在[-2,2]上恒成立,
∴a≤-3;
(Ⅱ)∵f(x)有两个不同的极值点m,n,
∴f′(x)=0有两个不等的实根,
即2x2+4x-a-1=0有两个不等的实根m,n,
∴△=16+8(a+1)>0,
解得a>-3,
由根与系数的关系可知m+n=2,mn=-$\frac{a+1}{2}$,
∵m+n≤mn+1,
∴-2≤-$\frac{a+1}{2}$+1,
解得a≤5,
∴-3<a≤5,
∵f(a)=(2a2-a-1)ea,
∴f′(a)=(2a2+3a-2)ea,
令f′(a)=0,解得a=-2或a=$\frac{1}{2}$,
∴f(-3)=20e-3,f(-2)=9e-2,f($\frac{1}{2}$)=-$\sqrt{e}$,f(5)=44e5,
∴f(a)的取值范围[-$\sqrt{e}$,44e5].
点评 本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识,考查运算求解能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
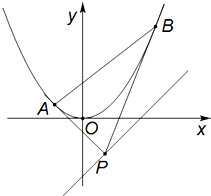 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{127}{64}$ | C. | $\frac{9}{4}$ | D. | $\frac{129}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32π | B. | 16π | C. | 12π | D. | $\frac{32}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
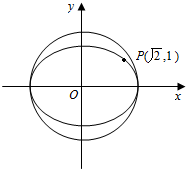 如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.
如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
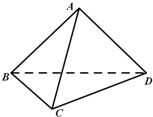 如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.
如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com